A Bayesian Approach for Predicting Food and Beverage Sales in Staff Canteens and Restaurants

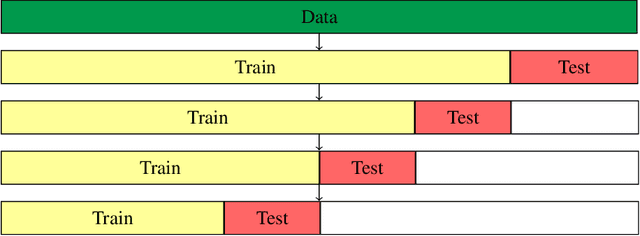
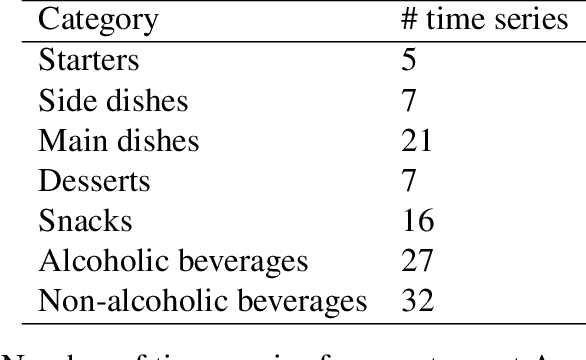
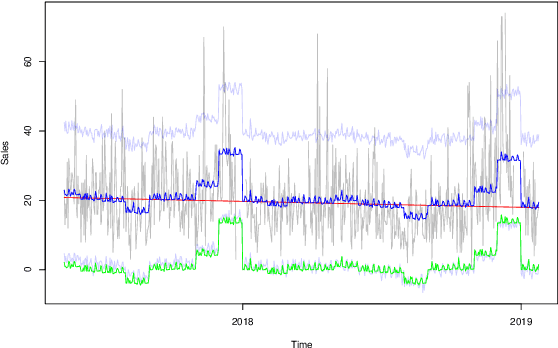
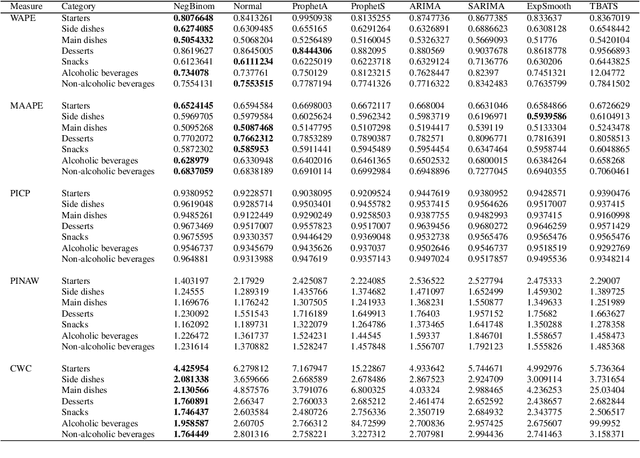
Accurate demand forecasting is one of the key aspects for successfully managing restaurants and staff canteens. In particular, properly predicting future sales of menu items allows a precise ordering of food stock. From an environmental point of view, this ensures maintaining a low level of pre-consumer food waste, while from the managerial point of view, this is critical to guarantee the profitability of the restaurant. Hence, we are interested in predicting future values of the daily sold quantities of given menu items. The corresponding time series show multiple strong seasonalities, trend changes, data gaps, and outliers. We propose a forecasting approach that is solely based on the data retrieved from Point of Sales systems and allows for a straightforward human interpretation. Therefore, we propose two generalized additive models for predicting the future sales. In an extensive evaluation, we consider two data sets collected at a casual restaurant and a large staff canteen consisting of multiple time series, that cover a period of 20 months, respectively. We show that the proposed models fit the features of the considered restaurant data. Moreover, we compare the predictive performance of our method against the performance of other well-established forecasting approaches.

Correlated Parameters to Accurately Measure Uncertainty in Deep Neural Networks

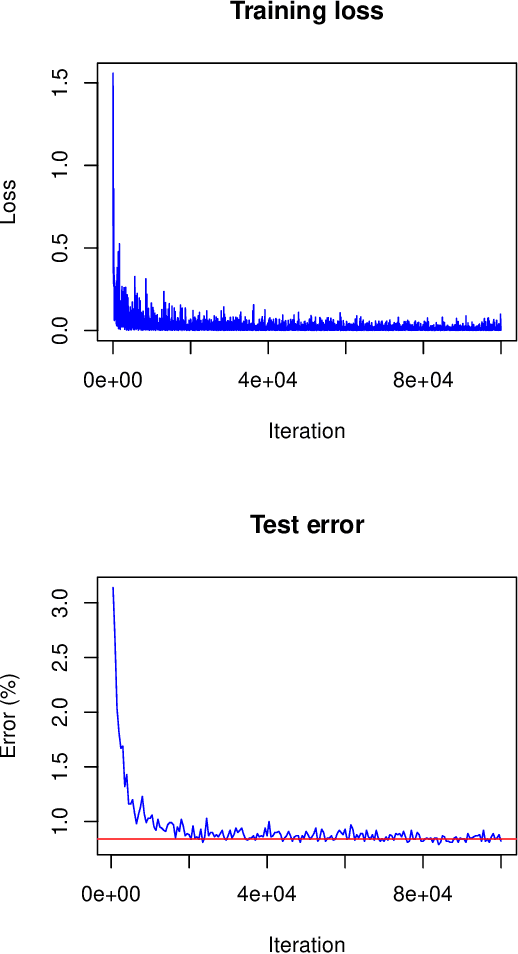
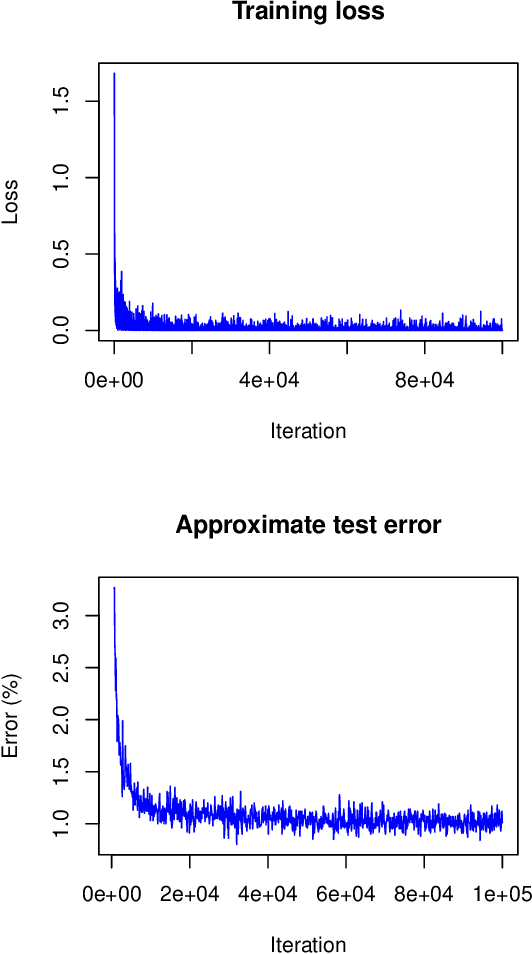
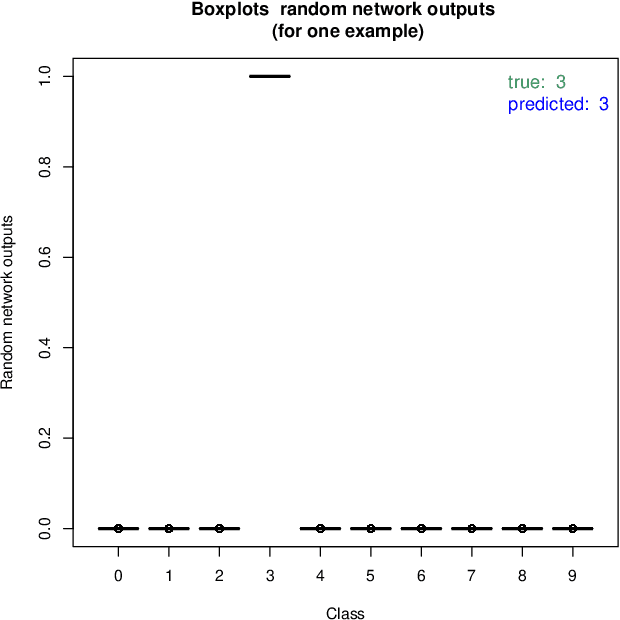
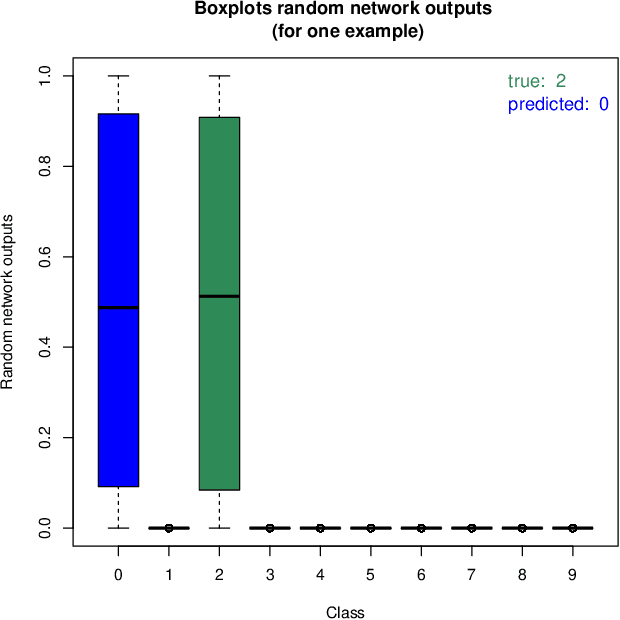
In this article a novel approach for training deep neural networks using Bayesian techniques is presented. The Bayesian methodology allows for an easy evaluation of model uncertainty and additionally is robust to overfitting. These are commonly the two main problems classical, i.e. non-Bayesian, architectures have to struggle with. The proposed approach applies variational inference in order to approximate the intractable posterior distribution. In particular, the variational distribution is defined as product of multiple multivariate normal distributions with tridiagonal covariance matrices. Each single normal distribution belongs either to the weights, or to the biases corresponding to one network layer. The layer-wise a posteriori variances are defined based on the corresponding expectation values and further the correlations are assumed to be identical. Therefore, only a few additional parameters need to be optimized compared to non-Bayesian settings. The novel approach is successfully evaluated on basis of the popular benchmark datasets MNIST and CIFAR-10.

Variational Inference to Measure Model Uncertainty in Deep Neural Networks

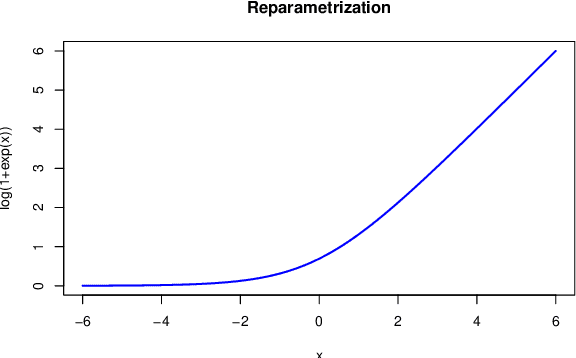
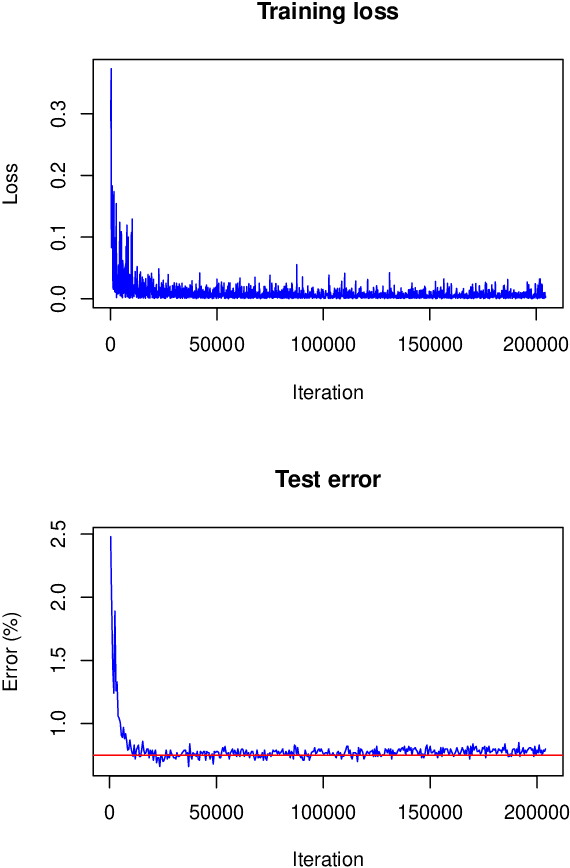
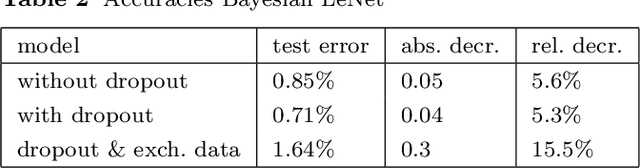
We present a novel approach for training deep neural networks in a Bayesian way. Classical, i.e. non-Bayesian, deep learning has two major drawbacks both originating from the fact that network parameters are considered to be deterministic. First, model uncertainty cannot be measured thus limiting the use of deep learning in many fields of application and second, training of deep neural networks is often hampered by overfitting. The proposed approach uses variational inference to approximate the intractable a posteriori distribution on basis of a normal prior. The variational density is designed in such a way that the a posteriori uncertainty of the network parameters is represented per network layer and depending on the estimated parameter expectation values. This way, only a few additional parameters need to be optimized compared to a non-Bayesian network. We apply this Bayesian approach to train and test the LeNet architecture on the MNIST dataset. Compared to classical deep learning, the test error is reduced by 15%. In addition, the trained model contains information about the parameter uncertainty in each layer. We show that this information can be used to calculate credible intervals for the prediction and to optimize the network architecture for a given training data set.