Iterative Quantum Feature Maps

Quantum machine learning models that leverage quantum circuits as quantum feature maps (QFMs) are recognized for their enhanced expressive power in learning tasks. Such models have demonstrated rigorous end-to-end quantum speedups for specific families of classification problems. However, deploying deep QFMs on real quantum hardware remains challenging due to circuit noise and hardware constraints. Additionally, variational quantum algorithms often suffer from computational bottlenecks, particularly in accurate gradient estimation, which significantly increases quantum resource demands during training. We propose Iterative Quantum Feature Maps (IQFMs), a hybrid quantum-classical framework that constructs a deep architecture by iteratively connecting shallow QFMs with classically computed augmentation weights. By incorporating contrastive learning and a layer-wise training mechanism, IQFMs effectively reduces quantum runtime and mitigates noise-induced degradation. In tasks involving noisy quantum data, numerical experiments show that IQFMs outperforms quantum convolutional neural networks, without requiring the optimization of variational quantum parameters. Even for a typical classical image classification benchmark, a carefully designed IQFMs achieves performance comparable to that of classical neural networks. This framework presents a promising path to address current limitations and harness the full potential of quantum-enhanced machine learning.

Resource-efficient equivariant quantum convolutional neural networks

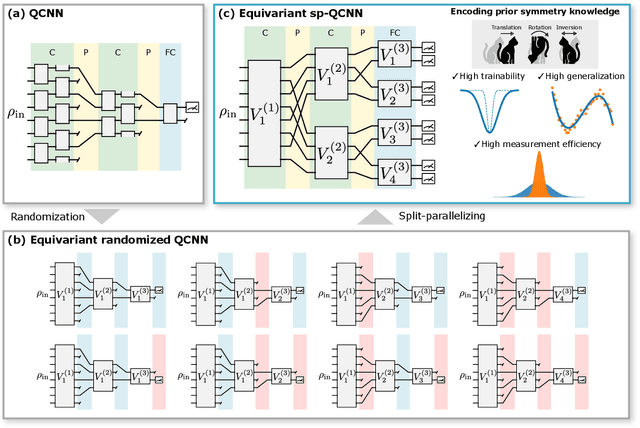
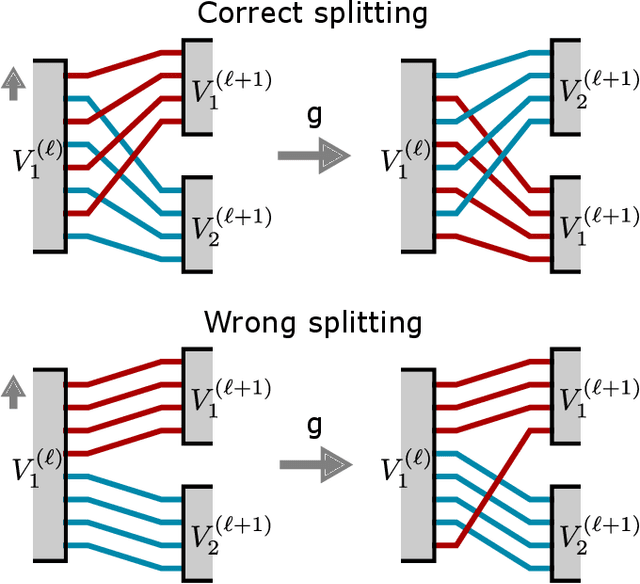
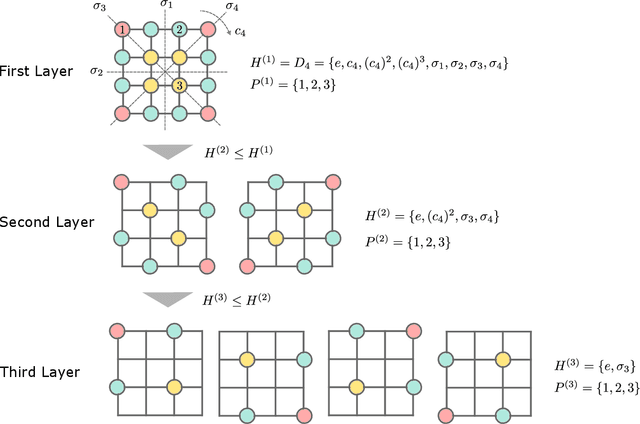
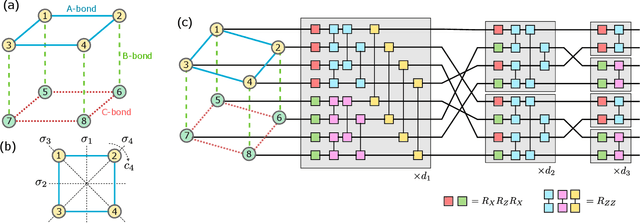
Equivariant quantum neural networks (QNNs) are promising quantum machine learning models that exploit symmetries to provide potential quantum advantages. Despite theoretical developments in equivariant QNNs, their implementation on near-term quantum devices remains challenging due to limited computational resources. This study proposes a resource-efficient model of equivariant quantum convolutional neural networks (QCNNs) called equivariant split-parallelizing QCNN (sp-QCNN). Using a group-theoretical approach, we encode general symmetries into our model beyond the translational symmetry addressed by previous sp-QCNNs. We achieve this by splitting the circuit at the pooling layer while preserving symmetry. This splitting structure effectively parallelizes QCNNs to improve measurement efficiency in estimating the expectation value of an observable and its gradient by order of the number of qubits. Our model also exhibits high trainability and generalization performance, including the absence of barren plateaus. Numerical experiments demonstrate that the equivariant sp-QCNN can be trained and generalized with fewer measurement resources than a conventional equivariant QCNN in a noisy quantum data classification task. Our results contribute to the advancement of practical quantum machine learning algorithms.

Trade-off between Gradient Measurement Efficiency and Expressivity in Deep Quantum Neural Networks

Quantum neural networks (QNNs) require an efficient training algorithm to achieve practical quantum advantages. A promising approach is the use of gradient-based optimization algorithms, where gradients are estimated through quantum measurements. However, it is generally difficult to efficiently measure gradients in QNNs because the quantum state collapses upon measurement. In this work, we prove a general trade-off between gradient measurement efficiency and expressivity in a wide class of deep QNNs, elucidating the theoretical limits and possibilities of efficient gradient estimation. This trade-off implies that a more expressive QNN requires a higher measurement cost in gradient estimation, whereas we can increase gradient measurement efficiency by reducing the QNN expressivity to suit a given task. We further propose a general QNN ansatz called the stabilizer-logical product ansatz (SLPA), which can reach the upper limit of the trade-off inequality by leveraging the symmetric structure of the quantum circuit. In learning an unknown symmetric function, the SLPA drastically reduces the quantum resources required for training while maintaining accuracy and trainability compared to a well-designed symmetric circuit based on the parameter-shift method. Our results not only reveal a theoretical understanding of efficient training in QNNs but also provide a standard and broadly applicable efficient QNN design.

Splitting and Parallelizing of Quantum Convolutional Neural Networks for Learning Translationally Symmetric Data

A quantum convolutional neural network (QCNN) is a promising quantum machine learning (QML) model to achieve quantum advantages in classically intractable problems. However, QCNN requires a large number of measurements for data learning, limiting its practical applications for large-scale problems. To relieve this requirement, we propose a novel architecture called split-parallelizing QCNN (sp-QCNN), which exploits the prior knowledge of quantum data for designing efficient circuits. This architecture draws inspiration from geometric quantum machine learning and targets translationally symmetric quantum data commonly encountered in condensed matter physics. By splitting the quantum circuit based on translational symmetry, sp-QCNN substantially parallelizes conventional QCNN without increasing the number of qubits and further improves the measurement efficiency by an order of the number of qubits. To demonstrate its effectiveness, we apply sp-QCNN to a quantum phase recognition task and show that it can achieve similar performance to conventional QCNN while considerably reducing the measurement resources required. Due to its high measurement efficiency, sp-QCNN can mitigate statistical errors in estimating the gradient of the loss function, thereby accelerating the learning process. These results open up new possibilities for incorporating the prior knowledge of data into the efficient design of QML models, leading to practical quantum advantages.