Koji Shimizu
Adaptive Constraint Integration for Simultaneously Optimizing Crystal Structures with Multiple Targeted Properties
Oct 11, 2024Abstract:In materials science, finding crystal structures that have targeted properties is crucial. While recent methodologies such as Bayesian optimization and deep generative models have made some advances on this issue, these methods often face difficulties in adaptively incorporating various constraints, such as electrical neutrality and targeted properties optimization, while keeping the desired specific crystal structure. To address these challenges, we have developed the Simultaneous Multi-property Optimization using Adaptive Crystal Synthesizer (SMOACS), which utilizes state-of-the-art property prediction models and their gradients to directly optimize input crystal structures for targeted properties simultaneously. SMOACS enables the integration of adaptive constraints into the optimization process without necessitating model retraining. Thanks to this feature, SMOACS has succeeded in simultaneously optimizing targeted properties while maintaining perovskite structures, even with models trained on diverse crystal types. We have demonstrated the band gap optimization while meeting a challenging constraint, that is, maintaining electrical neutrality in large atomic configurations up to 135 atom sites, where the verification of the electrical neutrality is challenging. The properties of the most promising materials have been confirmed by density functional theory calculations.
Efficient exploration of high-Tc superconductors by a gradient-based composition design
Mar 20, 2024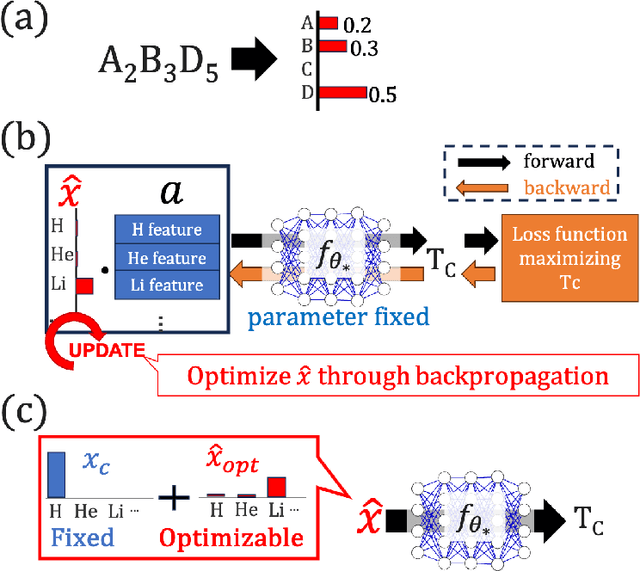
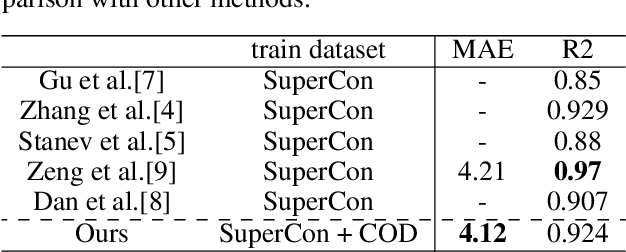
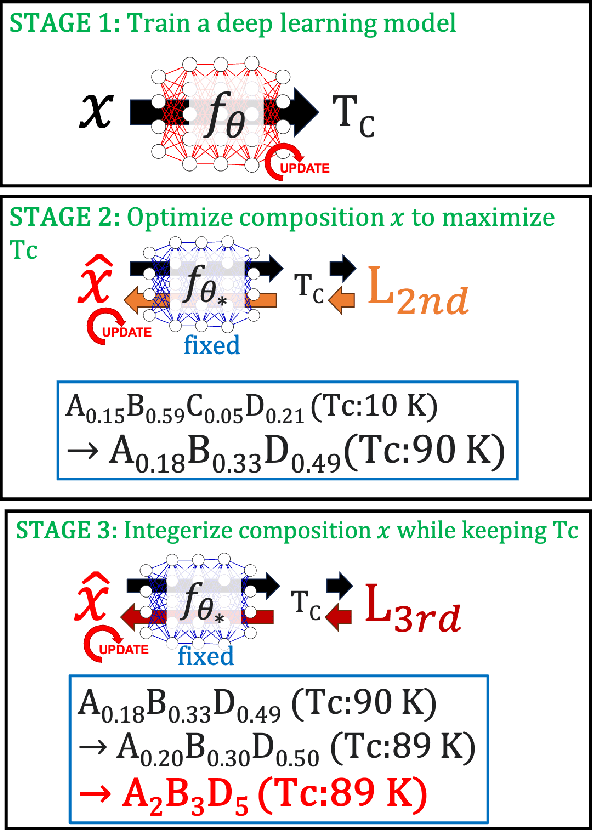
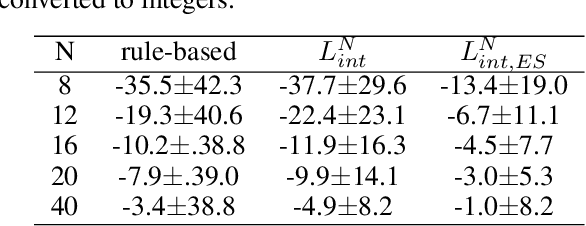
Abstract:We propose a material design method via gradient-based optimization on compositions, overcoming the limitations of traditional methods: exhaustive database searches and conditional generation models. It optimizes inputs via backpropagation, aligning the model's output closely with the target property and facilitating the discovery of unlisted materials and precise property determination. Our method is also capable of adaptive optimization under new conditions without retraining. Applying to exploring high-Tc superconductors, we identified potential compositions beyond existing databases and discovered new hydrogen superconductors via conditional optimization. This method is versatile and significantly advances material design by enabling efficient, extensive searches and adaptability to new constraints.
Enhancing Inverse Problem Solutions with Accurate Surrogate Simulators and Promising Candidates
Apr 26, 2023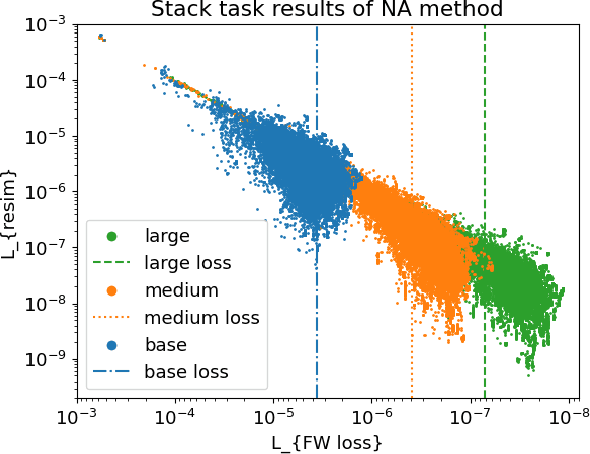

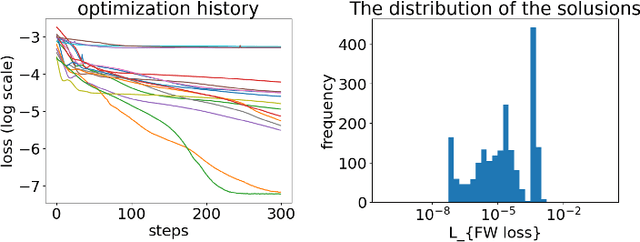

Abstract:Deep-learning inverse techniques have attracted significant attention in recent years. Among them, the neural adjoint (NA) method, which employs a neural network surrogate simulator, has demonstrated impressive performance in the design tasks of artificial electromagnetic materials (AEM). However, the impact of the surrogate simulators' accuracy on the solutions in the NA method remains uncertain. Furthermore, achieving sufficient optimization becomes challenging in this method when the surrogate simulator is large, and computational resources are limited. Additionally, the behavior under constraints has not been studied, despite its importance from the engineering perspective. In this study, we investigated the impact of surrogate simulators' accuracy on the solutions and discovered that the more accurate the surrogate simulator is, the better the solutions become. We then developed an extension of the NA method, named Neural Lagrangian (NeuLag) method, capable of efficiently optimizing a sufficient number of solution candidates. We then demonstrated that the NeuLag method can find optimal solutions even when handling sufficient candidates is difficult due to the use of a large and accurate surrogate simulator. The resimulation errors of the NeuLag method were approximately 1/50 compared to previous methods for three AEM tasks. Finally, we performed optimization under constraint using NA and NeuLag, and confirmed their potential in optimization with soft or hard constraints. We believe our method holds potential in areas that require large and accurate surrogate simulators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge