$ν^2$-Flows: Fast and improved neutrino reconstruction in multi-neutrino final states with conditional normalizing flows

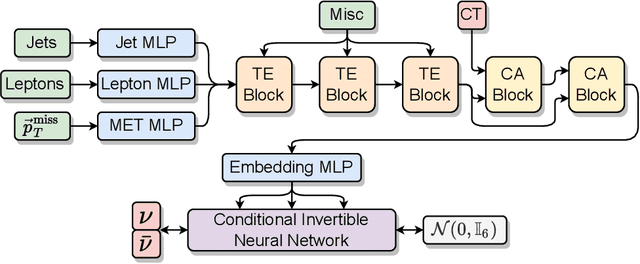
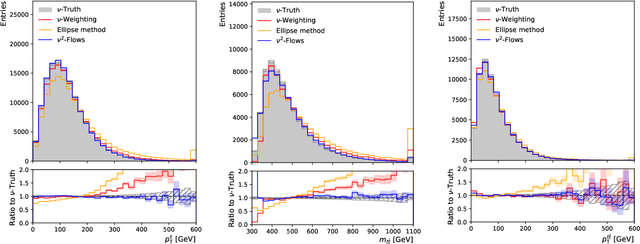
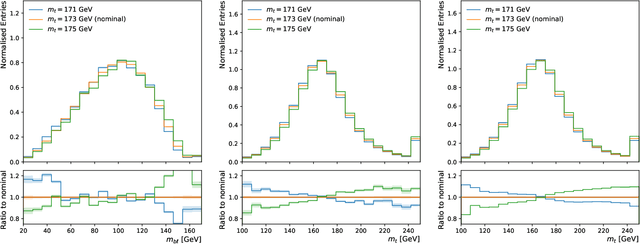
In this work we introduce $\nu^2$-Flows, an extension of the $\nu$-Flows method to final states containing multiple neutrinos. The architecture can natively scale for all combinations of object types and multiplicities in the final state for any desired neutrino multiplicities. In $t\bar{t}$ dilepton events, the momenta of both neutrinos and correlations between them are reconstructed more accurately than when using the most popular standard analytical techniques, and solutions are found for all events. Inference time is significantly faster than competing methods, and can be reduced further by evaluating in parallel on graphics processing units. We apply $\nu^2$-Flows to $t\bar{t}$ dilepton events and show that the per-bin uncertainties in unfolded distributions is much closer to the limit of performance set by perfect neutrino reconstruction than standard techniques. For the chosen double differential observables $\nu^2$-Flows results in improved statistical precision for each bin by a factor of 1.5 to 2 in comparison to the Neutrino Weighting method and up to a factor of four in comparison to the Ellipse approach.

Topological Reconstruction of Particle Physics Processes using Graph Neural Networks

We present a new approach, the Topograph, which reconstructs underlying physics processes, including the intermediary particles, by leveraging underlying priors from the nature of particle physics decays and the flexibility of message passing graph neural networks. The Topograph not only solves the combinatoric assignment of observed final state objects, associating them to their original mother particles, but directly predicts the properties of intermediate particles in hard scatter processes and their subsequent decays. In comparison to standard combinatoric approaches or modern approaches using graph neural networks, which scale exponentially or quadratically, the complexity of Topographs scales linearly with the number of reconstructed objects. We apply Topographs to top quark pair production in the all hadronic decay channel, where we outperform the standard approach and match the performance of the state-of-the-art machine learning technique.

PC-JeDi: Diffusion for Particle Cloud Generation in High Energy Physics

In this paper, we present a new method to efficiently generate jets in High Energy Physics called PC-JeDi. This method utilises score-based diffusion models in conjunction with transformers which are well suited to the task of generating jets as particle clouds due to their permutation equivariance. PC-JeDi achieves competitive performance with current state-of-the-art methods across several metrics that evaluate the quality of the generated jets. Although slower than other models, due to the large number of forward passes required by diffusion models, it is still substantially faster than traditional detailed simulation. Furthermore, PC-JeDi uses conditional generation to produce jets with a desired mass and transverse momentum for two different particles, top quarks and gluons.