Get our free extension to see links to code for papers anywhere online!

Chrome logo Add to Chrome

Firefox logo Add to Firefox
Picture for Kirsty Kitto

Kirsty Kitto

Quantum Mathematics in Artificial Intelligence


Feb 01, 2021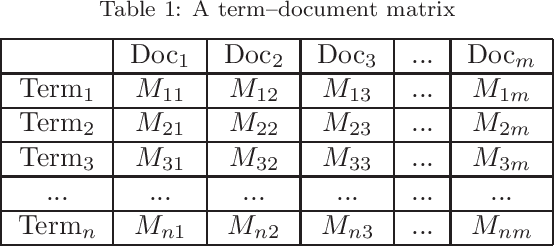
Dominic Widdows, Kirsty Kitto, Trevor Cohen

Figure 1 for Quantum Mathematics in Artificial Intelligence
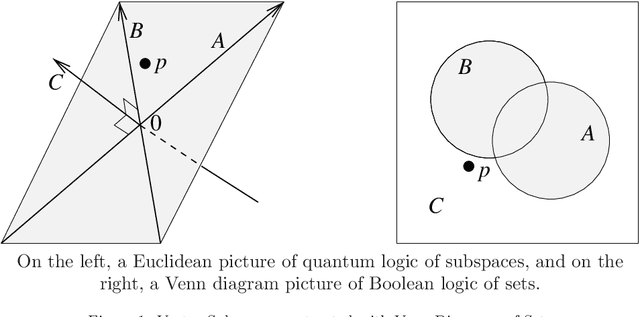
Figure 2 for Quantum Mathematics in Artificial Intelligence
* Manuscript updated to correct one author's email address, and with some extra references 
  Access Paper or Ask Questions

A probabilistic framework for analysing the compositionality of conceptual combinations


Nov 21, 2014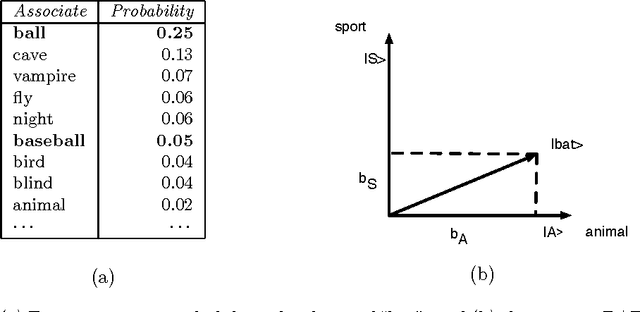
Peter D. Bruza, Kirsty Kitto, Brentyn J. Ramm, Laurianne Sitbon

Figure 1 for A probabilistic framework for analysing the compositionality of conceptual combinations
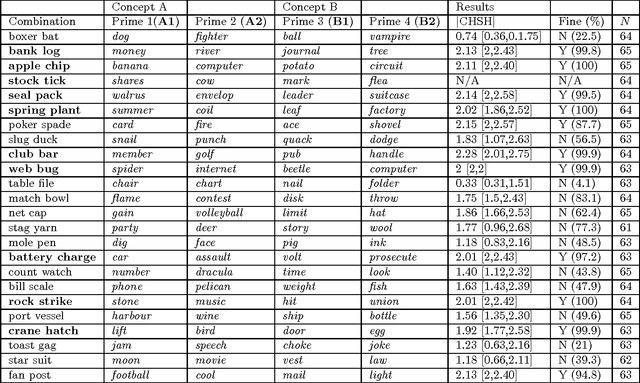
Figure 2 for A probabilistic framework for analysing the compositionality of conceptual combinations
Figure 3 for A probabilistic framework for analysing the compositionality of conceptual combinations
Figure 4 for A probabilistic framework for analysing the compositionality of conceptual combinations
* Revisions (Journal of Mathematical Psychology) 
  Access Paper or Ask Questions

Concept Combination and the Origins of Complex Cognition


Sep 28, 2013
Liane Gabora, Kirsty Kitto

Figure 1 for Concept Combination and the Origins of Complex Cognition
Figure 2 for Concept Combination and the Origins of Complex Cognition
Figure 3 for Concept Combination and the Origins of Complex Cognition
* In (E. Swan, Ed.) Origins of mind: Biosemiotics Series, Vol. 8 (pp. 361-382). Berlin: Springer 
 * 24 pages. arXiv admin note: substantial text overlap with arXiv:1308.5032 
  Access Paper or Ask Questions