DeepSpeech models show Human-like Performance and Processing of Cochlear Implant Inputs

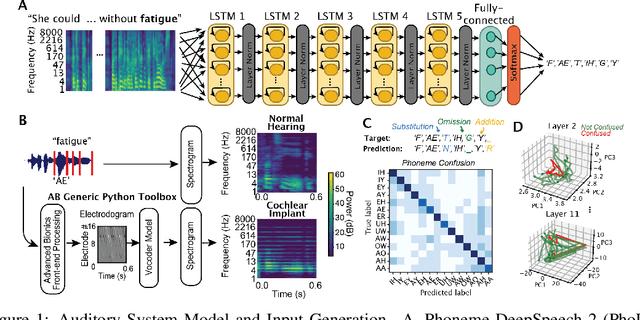
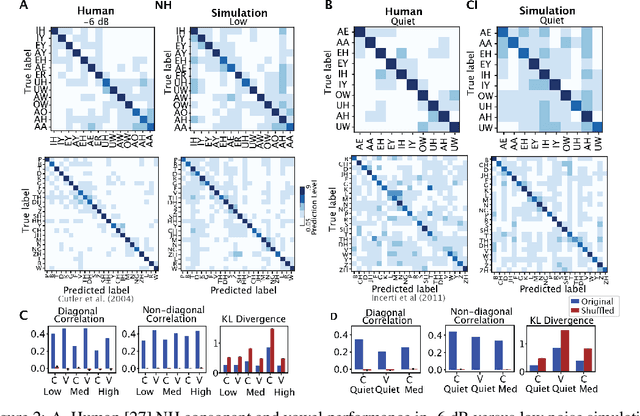
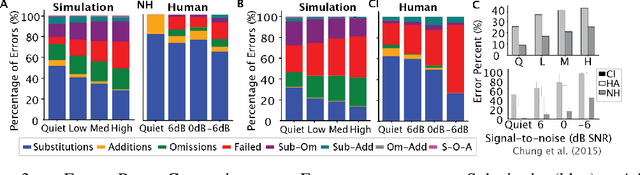
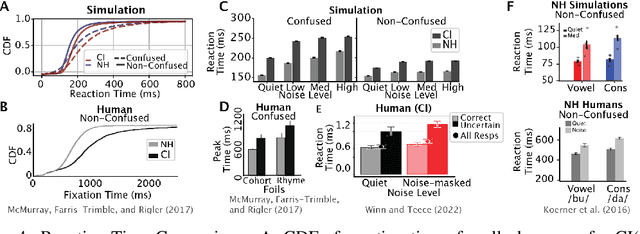
Cochlear implants(CIs) are arguably the most successful neural implant, having restored hearing to over one million people worldwide. While CI research has focused on modeling the cochlear activations in response to low-level acoustic features, we hypothesize that the success of these implants is due in large part to the role of the upstream network in extracting useful features from a degraded signal and learned statistics of language to resolve the signal. In this work, we use the deep neural network (DNN) DeepSpeech2, as a paradigm to investigate how natural input and cochlear implant-based inputs are processed over time. We generate naturalistic and cochlear implant-like inputs from spoken sentences and test the similarity of model performance to human performance on analogous phoneme recognition tests. Our model reproduces error patterns in reaction time and phoneme confusion patterns under noise conditions in normal hearing and CI participant studies. We then use interpretability techniques to determine where and when confusions arise when processing naturalistic and CI-like inputs. We find that dynamics over time in each layer are affected by context as well as input type. Dynamics of all phonemes diverge during confusion and comprehension within the same time window, which is temporally shifted backward in each layer of the network. There is a modulation of this signal during processing of CI which resembles changes in human EEG signals in the auditory stream. This reduction likely relates to the reduction of encoded phoneme identity. These findings suggest that we have a viable model in which to explore the loss of speech-related information in time and that we can use it to find population-level encoding signals to target when optimizing cochlear implant inputs to improve encoding of essential speech-related information and improve perception.

When does compositional structure yield compositional generalization? A kernel theory

Compositional generalization (the ability to respond correctly to novel combinations of familiar components) is thought to be a cornerstone of intelligent behavior. Compositionally structured (e.g. disentangled) representations are essential for this; however, the conditions under which they yield compositional generalization remain unclear. To address this gap, we present a general theory of compositional generalization in kernel models with fixed, potentially nonlinear representations (which also applies to neural networks in the "lazy regime"). We prove that these models are functionally limited to adding up values assigned to conjunctions/combinations of components that have been seen during training ("conjunction-wise additivity"), and identify novel compositionality failure modes that arise from the data and model structure, even for disentangled inputs. For models in the representation learning (or "rich") regime, we show that networks can generalize on an important non-additive task (associative inference), and give a mechanistic explanation for why. Finally, we validate our theory empirically, showing that it captures the behavior of deep neural networks trained on a set of compositional tasks. In sum, our theory characterizes the principles giving rise to compositional generalization in kernel models and shows how representation learning can overcome their limitations. We further provide a formally grounded, novel generalization class for compositional tasks that highlights fundamental differences in the required learning mechanisms (conjunction-wise additivity).

Spectral Inference Networks: Unifying Spectral Methods With Deep Learning

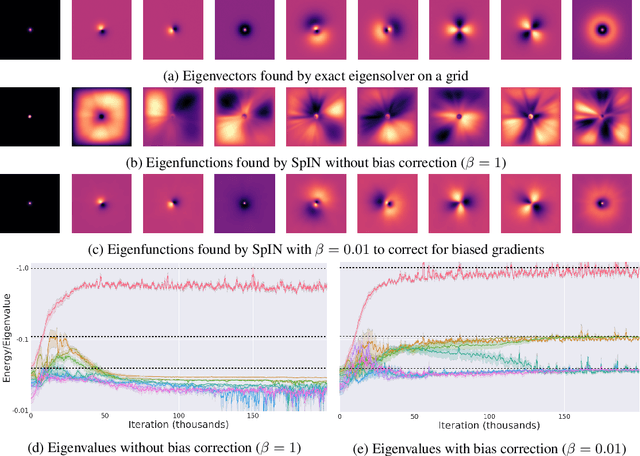
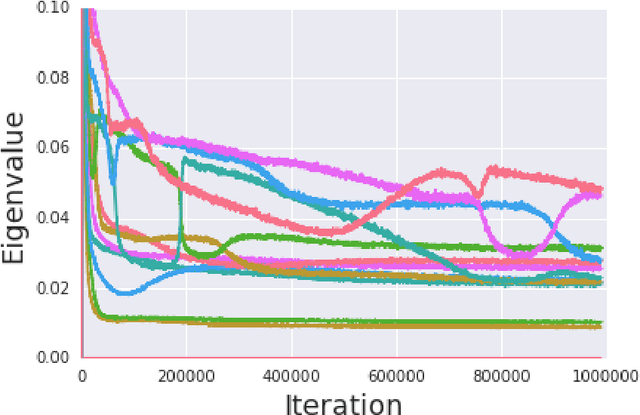
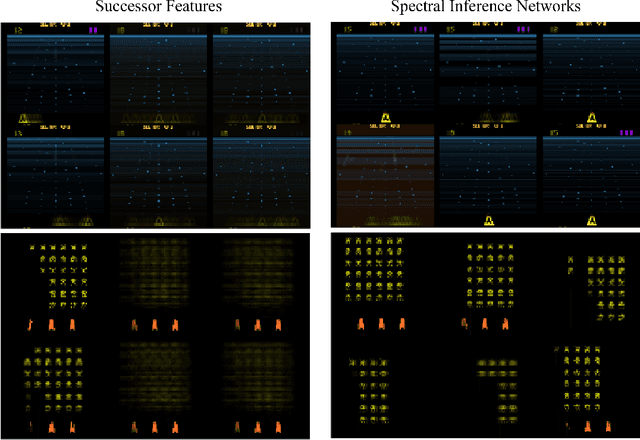
We present Spectral Inference Networks, a framework for learning eigenfunctions of linear operators by stochastic optimization. Spectral Inference Networks generalize Slow Feature Analysis to generic symmetric operators, and are closely related to Variational Monte Carlo methods from computational physics. As such, they can be a powerful tool for unsupervised representation learning from video or pairs of data. We derive a training algorithm for Spectral Inference Networks that addresses the bias in the gradients due to finite batch size and allows for online learning of multiple eigenfunctions. We show results of training Spectral Inference Networks on problems in quantum mechanics and feature learning for videos on synthetic datasets as well as the Arcade Learning Environment. Our results demonstrate that Spectral Inference Networks accurately recover eigenfunctions of linear operators, can discover interpretable representations from video and find meaningful subgoals in reinforcement learning environments.