Spectral Inference Networks: Unifying Spectral Methods With Deep Learning

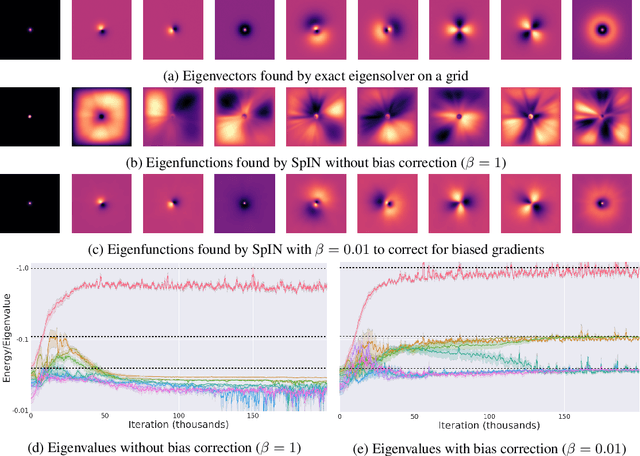
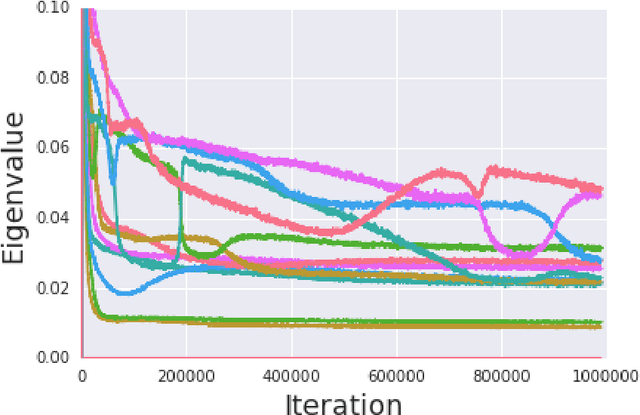
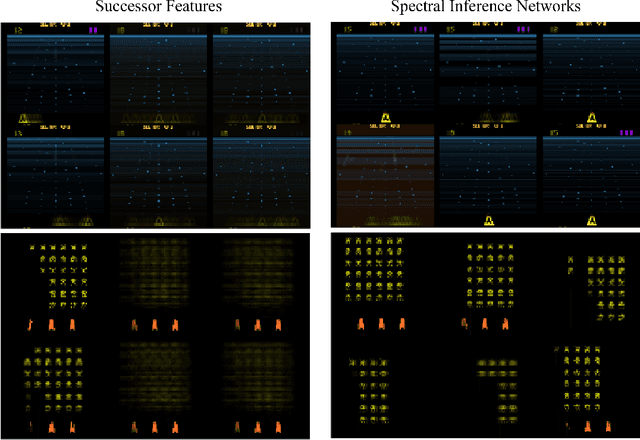
We present Spectral Inference Networks, a framework for learning eigenfunctions of linear operators by stochastic optimization. Spectral Inference Networks generalize Slow Feature Analysis to generic symmetric operators, and are closely related to Variational Monte Carlo methods from computational physics. As such, they can be a powerful tool for unsupervised representation learning from video or pairs of data. We derive a training algorithm for Spectral Inference Networks that addresses the bias in the gradients due to finite batch size and allows for online learning of multiple eigenfunctions. We show results of training Spectral Inference Networks on problems in quantum mechanics and feature learning for videos on synthetic datasets as well as the Arcade Learning Environment. Our results demonstrate that Spectral Inference Networks accurately recover eigenfunctions of linear operators, can discover interpretable representations from video and find meaningful subgoals in reinforcement learning environments.