Khoi Minh Nguyen-Duy
Adaptive-saturated RNN: Remember more with less instability
Apr 24, 2023



Abstract:Orthogonal parameterization is a compelling solution to the vanishing gradient problem (VGP) in recurrent neural networks (RNNs). With orthogonal parameters and non-saturated activation functions, gradients in such models are constrained to unit norms. On the other hand, although the traditional vanilla RNNs are seen to have higher memory capacity, they suffer from the VGP and perform badly in many applications. This work proposes Adaptive-Saturated RNNs (asRNN), a variant that dynamically adjusts its saturation level between the two mentioned approaches. Consequently, asRNN enjoys both the capacity of a vanilla RNN and the training stability of orthogonal RNNs. Our experiments show encouraging results of asRNN on challenging sequence learning benchmarks compared to several strong competitors. The research code is accessible at https://github.com/ndminhkhoi46/asRNN/.
* 8 pages, 2 figures, 5 tables, ICLR 2023 Tiny Paper Track
DPER: Efficient Parameter Estimation for Randomly Missing Data
Jun 06, 2021
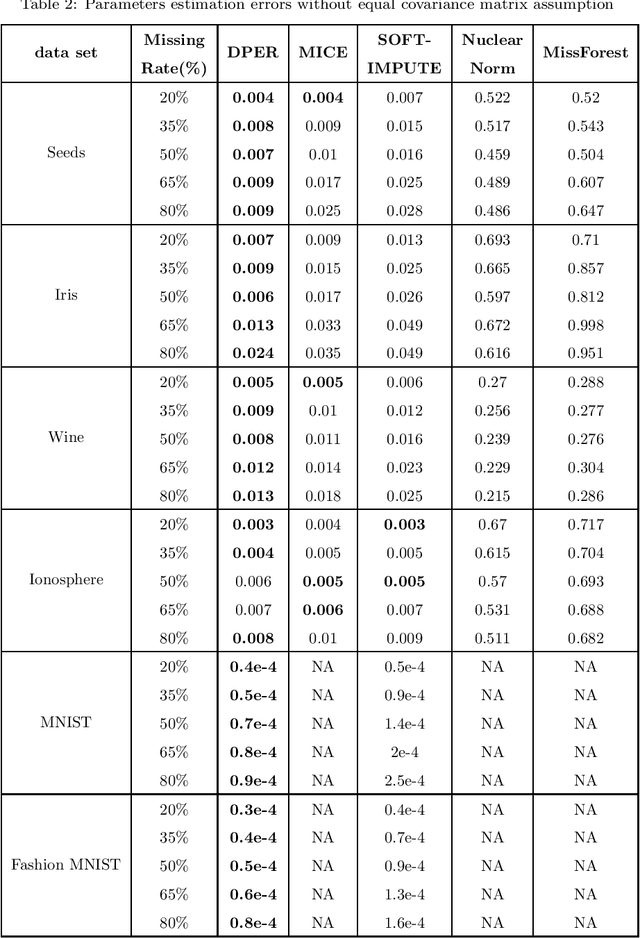
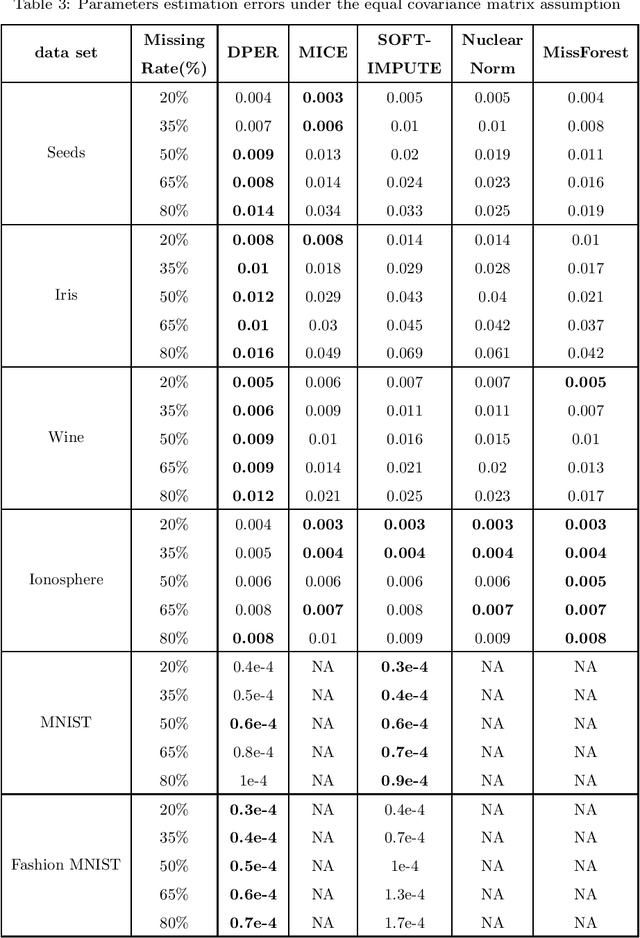
Abstract:The missing data problem has been broadly studied in the last few decades and has various applications in different areas such as statistics or bioinformatics. Even though many methods have been developed to tackle this challenge, most of those are imputation techniques that require multiple iterations through the data before yielding convergence. In addition, such approaches may introduce extra biases and noises to the estimated parameters. In this work, we propose novel algorithms to find the maximum likelihood estimates (MLEs) for a one-class/multiple-class randomly missing data set under some mild assumptions. As the computation is direct without any imputation, our algorithms do not require multiple iterations through the data, thus promising to be less time-consuming than other methods while maintaining superior estimation performance. We validate these claims by empirical results on various data sets of different sizes and release all codes in a GitHub repository to contribute to the research community related to this problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge