Kenny Schlegel
HDC-MiniROCKET: Explicit Time Encoding in Time Series Classification with Hyperdimensional Computing
Feb 16, 2022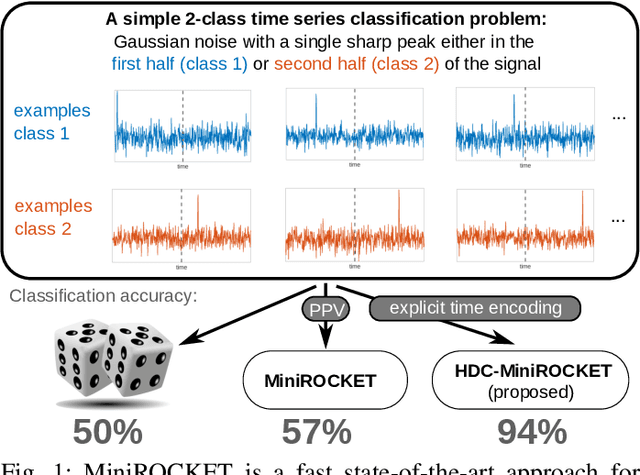
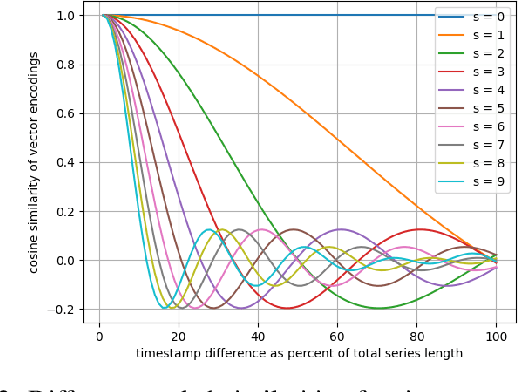
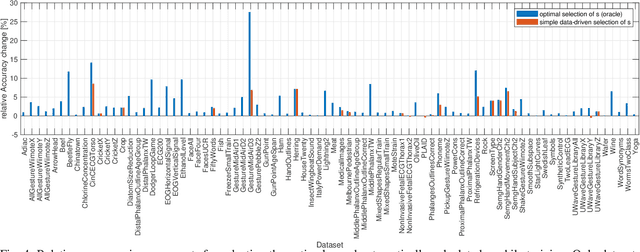
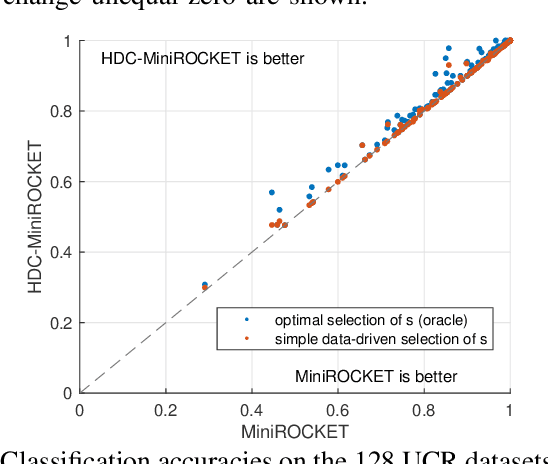
Abstract:Classification of time series data is an important task for many application domains. One of the best existing methods for this task, in terms of accuracy and computation time, is MiniROCKET. In this work, we extend this approach to provide better global temporal encodings using hyperdimensional computing (HDC) mechanisms. HDC (also known as Vector Symbolic Architectures, VSA) is a general method to explicitly represent and process information in high-dimensional vectors. It has previously been used successfully in combination with deep neural networks and other signal processing algorithms. We argue that the internal high-dimensional representation of MiniROCKET is well suited to be complemented by the algebra of HDC. This leads to a more general formulation, HDC-MiniROCKET, where the original algorithm is only a special case. We will discuss and demonstrate that HDC-MiniROCKET can systematically overcome catastrophic failures of MiniROCKET on simple synthetic datasets. These results are confirmed by experiments on the 128 datasets from the UCR time series classification benchmark. The extension with HDC can achieve considerably better results on datasets with high temporal dependence without increasing the computational effort for inference.
A comparison of Vector Symbolic Architectures
Feb 20, 2020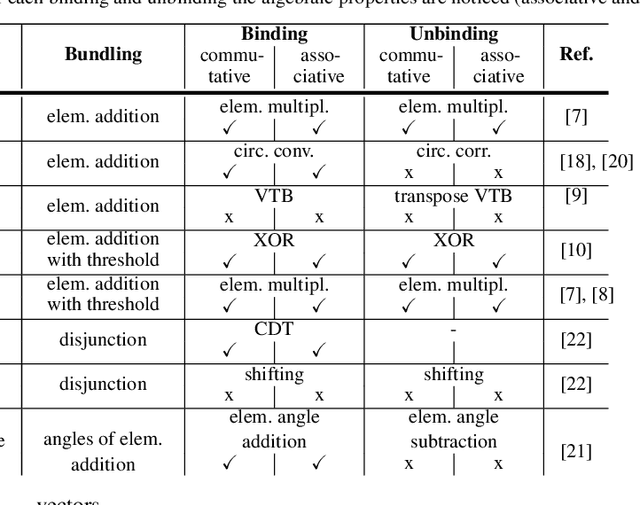
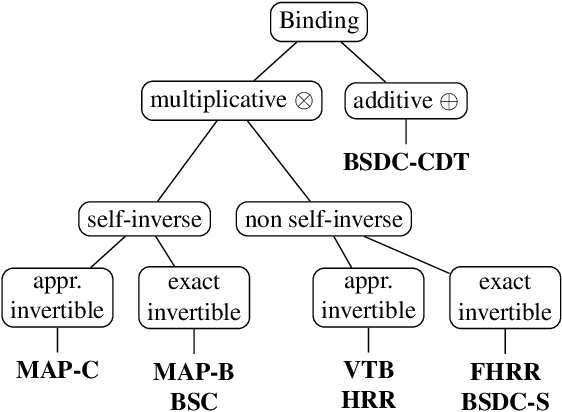
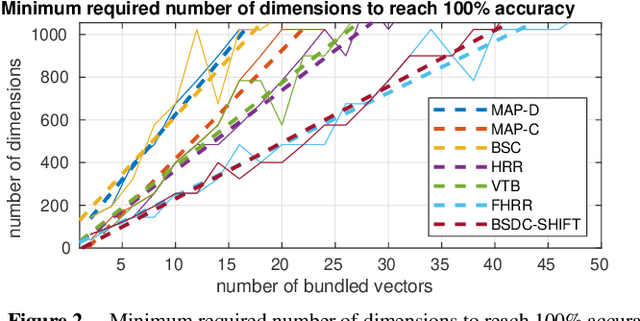

Abstract:Vector Symbolic Architectures (VSAs) combine a high-dimensional vector space with a set of carefully designed operators in order to perform symbolic computations with large numerical vectors. Major goals are the exploitation of their representational power and ability to deal with fuzziness and ambiguity. Over the past years, VSAs have been applied to a broad range of tasks and several VSA implementations have been proposed. The available implementations differ in the underlying vector space (e.g., binary vectors or complex-valued vectors) and the particular implementations of the required VSA operators - with important ramifications for the properties of these architectures. For example, not every VSA is equally well suited to address each task, including complete incompatibility. In this paper, we give an overview of eight available VSA implementations and discuss their commonalities and differences in the underlying vector space, bundling, and binding/unbinding operations. We create a taxonomy of available binding/unbinding operations and show an important ramification for non self-inverse binding operation using an example from analogical reasoning. A main contribution is the experimental comparison of the available implementations regarding (1) the capacity of bundles, (2) the approximation quality of non-exact unbinding operations, and (3) the influence of combined binding and bundling operations on the query answering performance. We expect this systematization and comparison to be relevant for development and evaluation of new VSAs, but most importantly, to support the selection of an appropriate VSA for a particular task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge