A comparison of Vector Symbolic Architectures

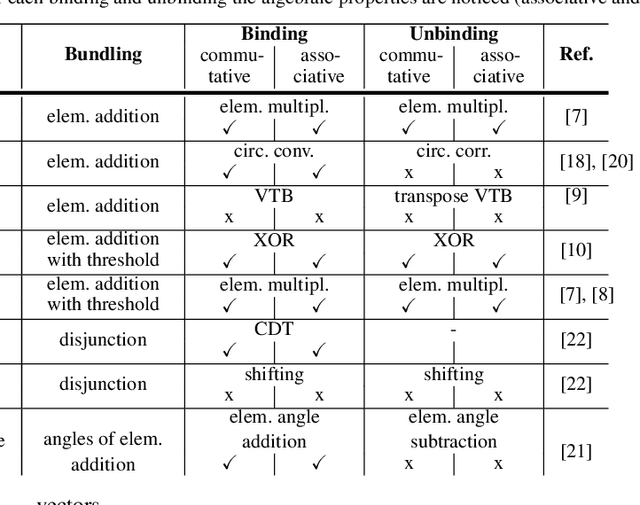
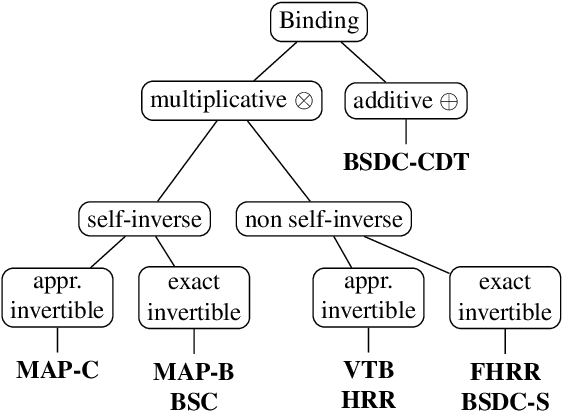
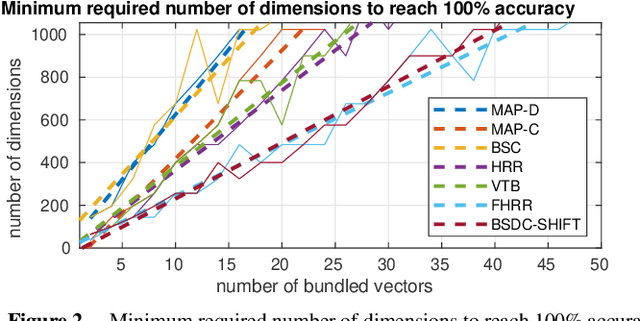
Vector Symbolic Architectures (VSAs) combine a high-dimensional vector space with a set of carefully designed operators in order to perform symbolic computations with large numerical vectors. Major goals are the exploitation of their representational power and ability to deal with fuzziness and ambiguity. Over the past years, VSAs have been applied to a broad range of tasks and several VSA implementations have been proposed. The available implementations differ in the underlying vector space (e.g., binary vectors or complex-valued vectors) and the particular implementations of the required VSA operators - with important ramifications for the properties of these architectures. For example, not every VSA is equally well suited to address each task, including complete incompatibility. In this paper, we give an overview of eight available VSA implementations and discuss their commonalities and differences in the underlying vector space, bundling, and binding/unbinding operations. We create a taxonomy of available binding/unbinding operations and show an important ramification for non self-inverse binding operation using an example from analogical reasoning. A main contribution is the experimental comparison of the available implementations regarding (1) the capacity of bundles, (2) the approximation quality of non-exact unbinding operations, and (3) the influence of combined binding and bundling operations on the query answering performance. We expect this systematization and comparison to be relevant for development and evaluation of new VSAs, but most importantly, to support the selection of an appropriate VSA for a particular task.