Using physics-based simulation towards eliminating empiricism in extraterrestrial terramechanics applications

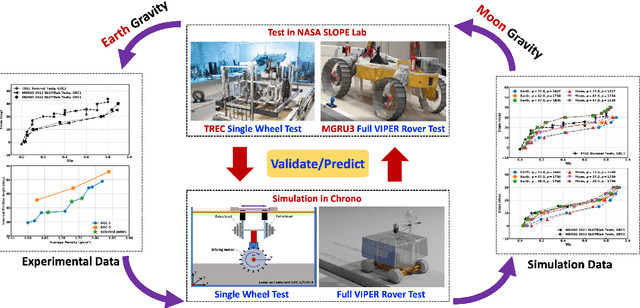
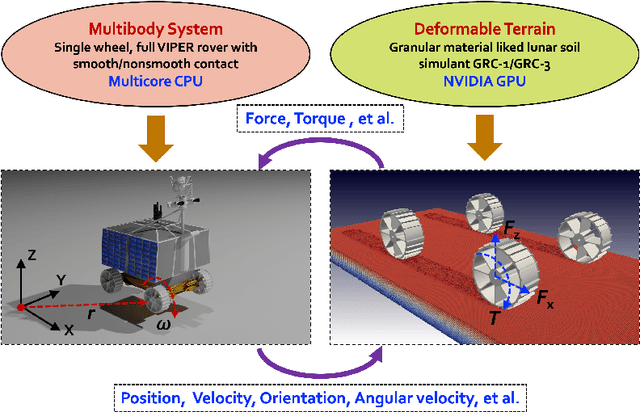
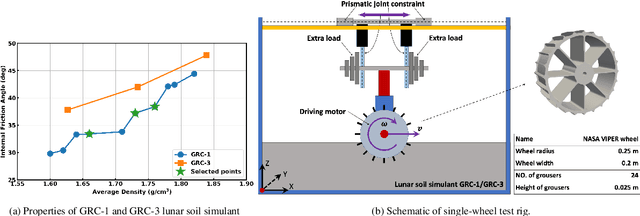
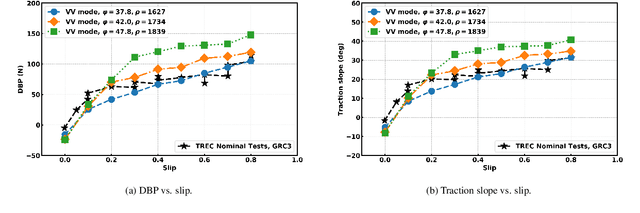
Recently, there has been a surge of international interest in extraterrestrial exploration targeting the Moon, Mars, the moons of Mars, and various asteroids. This contribution discusses how current state-of-the-art Earth-based testing for designing rovers and landers for these missions currently leads to overly optimistic conclusions about the behavior of these devices upon deployment on the targeted celestial bodies. The key misconception is that gravitational offset is necessary during the \textit{terramechanics} testing of rover and lander prototypes on Earth. The body of evidence supporting our argument is tied to a small number of studies conducted during parabolic flights and insights derived from newly revised scaling laws. We argue that what has prevented the community from fully diagnosing the problem at hand is the absence of effective physics-based models capable of simulating terramechanics under low gravity conditions. We developed such a physics-based simulator and utilized it to gauge the mobility of early prototypes of the Volatiles Investigating Polar Exploration Rover (VIPER), which is slated to depart for the Moon in November 2024. This contribution discusses the results generated by this simulator, how they correlate with physical test results from the NASA-Glenn SLOPE lab, and the fallacy of the gravitational offset in rover and lander testing. The simulator developed is open sourced and made publicly available for unfettered use; it can support principled studies that extend beyond trafficability analysis to provide insights into in-situ resource utilization activities, e.g., digging, bulldozing, and berming in low gravity.

Topology optimization with physics-informed neural networks: application to noninvasive detection of hidden geometries

Detecting hidden geometrical structures from surface measurements under electromagnetic, acoustic, or mechanical loading is the goal of noninvasive imaging techniques in medical and industrial applications. Solving the inverse problem can be challenging due to the unknown topology and geometry, the sparsity of the data, and the complexity of the physical laws. Physics-informed neural networks (PINNs) have shown promise as a simple-yet-powerful tool for problem inversion, but they have yet to be applied to general problems with a priori unknown topology. Here, we introduce a topology optimization framework based on PINNs that solves geometry detection problems without prior knowledge of the number or types of shapes. We allow for arbitrary solution topology by representing the geometry using a material density field that approaches binary values thanks to a novel eikonal regularization. We validate our framework by detecting the number, locations, and shapes of hidden voids and inclusions in linear and nonlinear elastic bodies using measurements of outer surface displacement from a single mechanical loading experiment. Our methodology opens a pathway for PINNs to solve various engineering problems targeting geometry optimization.