Nonlinearity and Uncertainty Informed Moment-Matching Gaussian Mixture Splitting

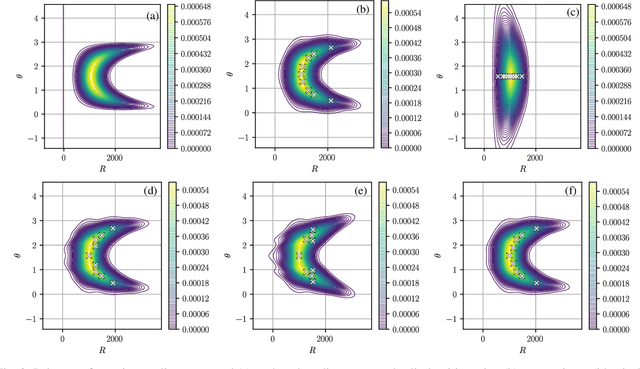
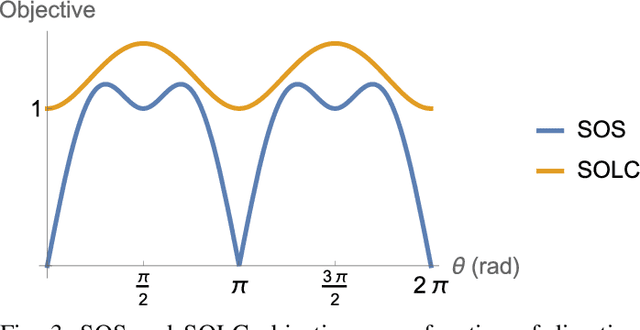
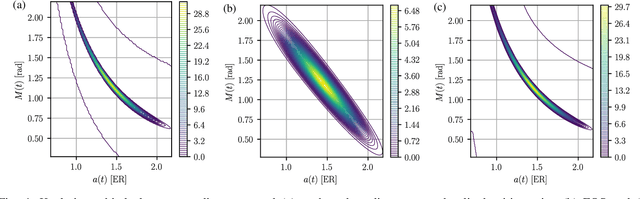
Many problems in navigation and tracking require increasingly accurate characterizations of the evolution of uncertainty in nonlinear systems. Nonlinear uncertainty propagation approaches based on Gaussian mixture density approximations offer distinct advantages over sampling based methods in their computational cost and continuous representation. State-of-the-art Gaussian mixture approaches are adaptive in that individual Gaussian mixands are selectively split into mixtures to yield better approximations of the true propagated distribution. Despite the importance of the splitting process to accuracy and computational efficiency, relatively little work has been devoted to mixand selection and splitting direction optimization. The first part of this work presents splitting methods that preserve the mean and covariance of the original distribution. Then, we present and compare a number of novel heuristics for selecting the splitting direction. The choice of splitting direction is informed by the initial uncertainty distribution, properties of the nonlinear function through which the original distribution is propagated, and a whitening based natural scaling method to avoid dependence of the splitting direction on the scaling of coordinates. We compare these novel heuristics to existing techniques in three distinct examples involving Cartesian to polar coordinate transformation, Keplerian orbital element propagation, and uncertainty propagation in the circular restricted three-body problem.

Split Happens! Imprecise and Negative Information in Gaussian Mixture Random Finite Set Filtering

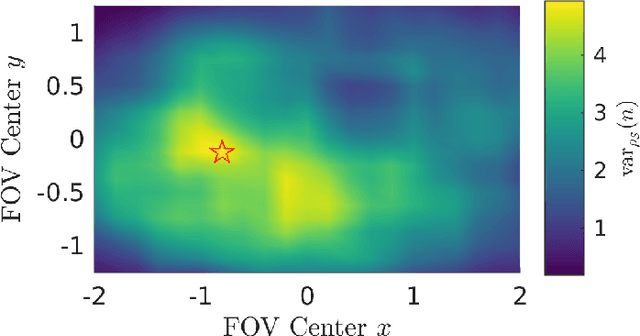
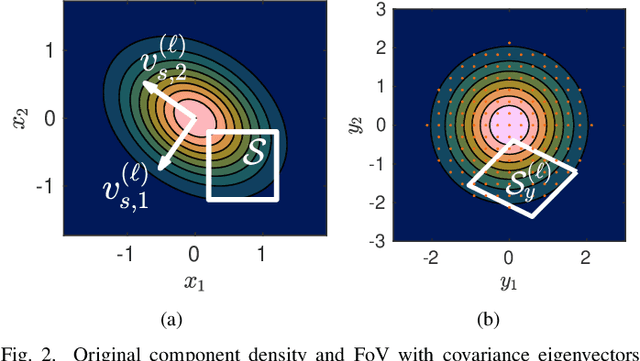
In object tracking and state estimation problems, ambiguous evidence such as imprecise measurements and the absence of detections can contain valuable information and thus be leveraged to further refine the probabilistic belief state. In particular, knowledge of a sensor's bounded field-of-view can be exploited to incorporate evidence of where an object was not observed. This paper presents a systematic approach for incorporating knowledge of the field-of-view geometry and position and object inclusion/exclusion evidence into object state densities and random finite set multi-object cardinality distributions. The resulting state estimation problem is nonlinear and solved using a new Gaussian mixture approximation based on recursive component splitting. Based on this approximation, a novel Gaussian mixture Bernoulli filter for imprecise measurements is derived and demonstrated in a tracking problem using only natural language statements as inputs. This paper also considers the relationship between bounded fields-of-view and cardinality distributions for a representative selection of multi-object distributions, which can be used for sensor planning, as is demonstrated through a problem involving a multi-Bernoulli process with up to one-hundred potential objects.

Cell Multi-Bernoulli Sensor Control for Multi-object Search-While-Tracking

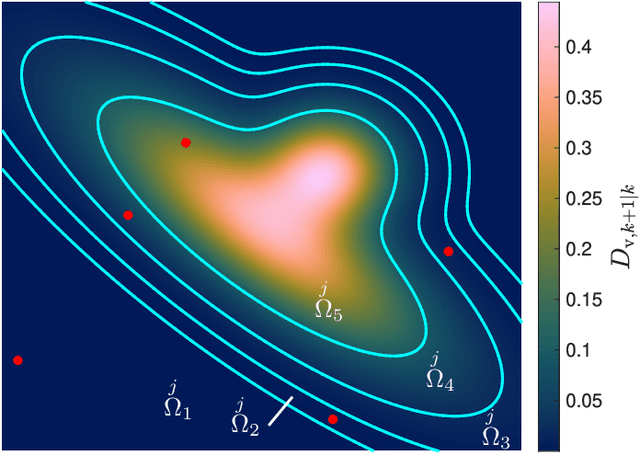
Information driven control can be used to develop intelligent sensors that can optimize their measurement value based on environmental feedback. In object tracking applications, sensor actions are chosen based on the expected reduction in uncertainty also known as information gain. Random finite set (RFS) theory provides a formalism for quantifying and estimating information gain in multi-object tracking problems. However, estimating information gain in these applications remains computationally challenging. This paper presents a new tractable approximation of the RFS expected information gain applicable to sensor control for multi-object search and tracking. Unlike existing RFS approaches, the approximation presented in this paper accounts for noisy measurements, missed detections, false alarms, and object appearance/disappearance. The effectiveness of the information driven sensor control is demonstrated through a multi-vehicle search-while-tracking experiment using real video data from a remote optical sensor.