Nonlinearity and Uncertainty Informed Moment-Matching Gaussian Mixture Splitting

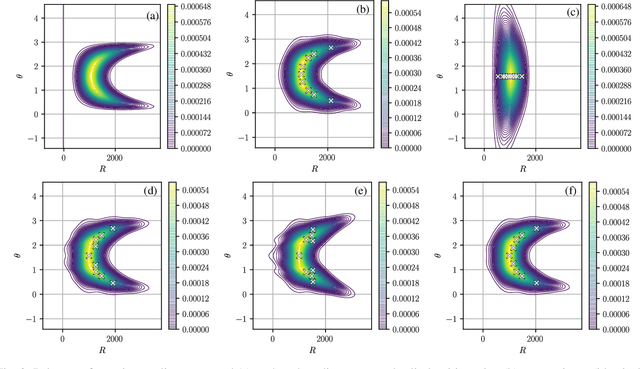
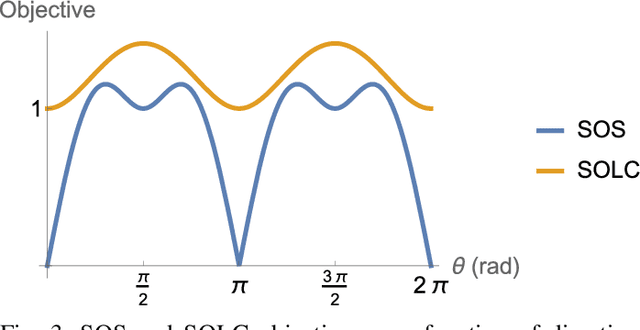
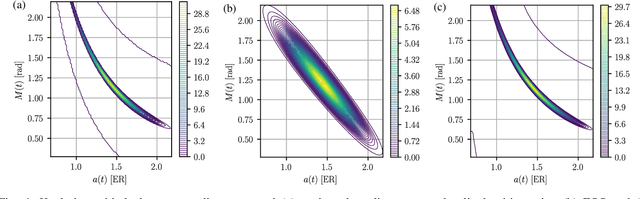
Many problems in navigation and tracking require increasingly accurate characterizations of the evolution of uncertainty in nonlinear systems. Nonlinear uncertainty propagation approaches based on Gaussian mixture density approximations offer distinct advantages over sampling based methods in their computational cost and continuous representation. State-of-the-art Gaussian mixture approaches are adaptive in that individual Gaussian mixands are selectively split into mixtures to yield better approximations of the true propagated distribution. Despite the importance of the splitting process to accuracy and computational efficiency, relatively little work has been devoted to mixand selection and splitting direction optimization. The first part of this work presents splitting methods that preserve the mean and covariance of the original distribution. Then, we present and compare a number of novel heuristics for selecting the splitting direction. The choice of splitting direction is informed by the initial uncertainty distribution, properties of the nonlinear function through which the original distribution is propagated, and a whitening based natural scaling method to avoid dependence of the splitting direction on the scaling of coordinates. We compare these novel heuristics to existing techniques in three distinct examples involving Cartesian to polar coordinate transformation, Keplerian orbital element propagation, and uncertainty propagation in the circular restricted three-body problem.