Robust Spatiotemporal Fusion of Satellite Images: A Constrained Convex Optimization Approach

This paper proposes a novel spatiotemporal (ST) fusion framework for satellite images, named Robust Optimization-based Spatiotemporal Fusion (ROSTF). ST fusion is a promising approach to resolve a trade-off between the temporal and spatial resolution of satellite images. Although many ST fusion methods have been proposed, most of them are not designed to explicitly account for noise in observed images, despite the inevitable influence of noise caused by the measurement equipment and environment. Our ROSTF addresses this challenge by treating the noise removal of the observed images and the estimation of the target high-resolution image as a single optimization problem. Specifically, first, we define observation models for satellite images possibly contaminated with random noise, outliers, and/or missing values, and then introduce certain assumptions that would naturally hold between the observed images and the target high-resolution image. Then, based on these models and assumptions, we formulate the fusion problem as a constrained optimization problem and develop an efficient algorithm based on a preconditioned primal-dual splitting method for solving the problem. The performance of ROSTF was verified using simulated and real data. The results show that ROSTF performs comparably to several state-of-the-art ST fusion methods in noiseless cases and outperforms them in noisy cases.

Graph Signal Sampling Under Smoothness Priors: A Difference-of-Convex Approach

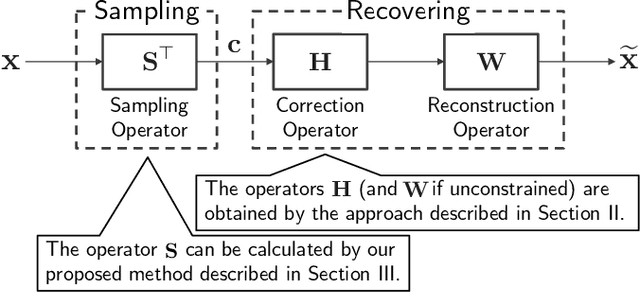
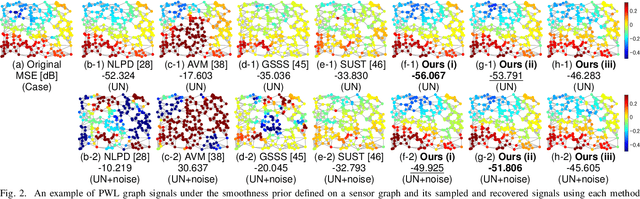
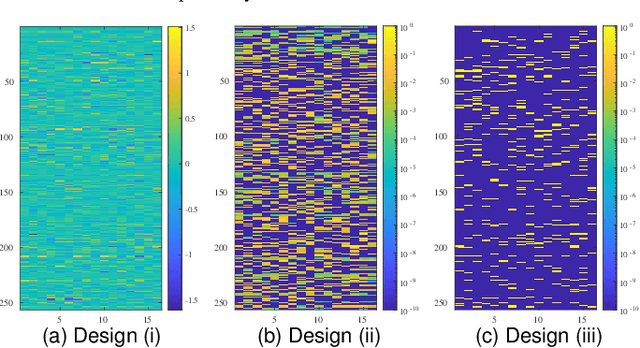
This paper proposes a method for properly sampling graph signals under smoothness priors. Unlike many existing approaches that assume bandlimited graph signals, our method designs a sampling operator for graph signals that are not necessarily bandlimited based on the generalized sampling theory. First, we formulate the sampling operator design under smoothness priors as a feasibility problem. Then, we transform this problem into a Difference-of-Convex (DC) problem by relaxing a certain invertibility constraint in the original problem using the nuclear norm. Furthermore, we develop an efficient algorithm to solve this DC problem based on the proximal linearized difference-of-convex algorithm and guarantee its convergence to a critical point of the problem. Finally, we demonstrate the effectiveness of our method for several graph signal models through sampling-and-reconstruction experiments.

Robust Constrained Hyperspectral Unmixing Using Reconstructed-Image Regularization

Hyperspectral (HS) unmixing is the process of decomposing an HS image into material-specific spectra (endmembers) and their spatial distributions (abundance maps). Existing unmixing methods have two limitations with respect to noise robustness. First, if the input HS image is highly noisy, even if the balance between sparse and piecewise-smooth regularizations for abundance maps is carefully adjusted, noise may remain in the estimated abundance maps or undesirable artifacts may appear. Second, existing methods do not explicitly account for the effects of stripe noise, which is common in HS measurements, in their formulations, resulting in significant degradation of unmixing performance when such noise is present in the input HS image. To overcome these limitations, we propose a new robust hyperspectral unmixing method based on constrained convex optimization. Our method employs, in addition to the two regularizations for the abundance maps, regularizations for the HS image reconstructed by mixing the estimated abundance maps and endmembers. This strategy makes the unmixing process much more robust in highly-noisy scenarios, under the assumption that the abundance maps used to reconstruct the HS image with desirable spatio-spectral structure are also expected to have desirable properties. Furthermore, our method is designed to accommodate a wider variety of noise including stripe noise. To solve the formulated optimization problem, we develop an efficient algorithm based on a preconditioned primal-dual splitting method, which can automatically determine appropriate stepsizes based on the problem structure. Experiments on synthetic and real HS images demonstrate the advantages of our method over existing methods.

Variable-Wise Diagonal Preconditioning for Primal-Dual Splitting: Design and Applications

This paper proposes a method of designing appropriate diagonal preconditioners for a preconditioned primal-dual splitting method (P-PDS). P-PDS can efficiently solve various types of convex optimization problems arising in signal processing and image processing. Since the appropriate diagonal preconditioners that accelerate the convergence of P-PDS vary greatly depending on the structure of the target optimization problem, a design method of diagonal preconditioners for PPDS has been proposed to determine them automatically from the problem structure. However, the existing method has two limitations: it requires direct access to all elements of the matrices representing the linear operators involved in the target optimization problem, and it is element-wise preconditioning, which makes certain types of proximity operators impossible to compute analytically. To overcome these limitations, we establish an Operator-norm-based design method of Variable-wise Diagonal Preconditioning (OVDP). First, the diagonal preconditioners constructed by OVDP are defined using only the operator norm or its upper bound of the linear operator thus eliminating the need for their explicit matrix representations. Furthermore, since our method is variable-wise preconditioning, it keeps all proximity operators efficiently computable. We also prove that our preconditioners satisfy the convergence conditions of PPDS. Finally, we demonstrate the effectiveness and utility of our method through applications to hyperspectral image mixed noise removal, hyperspectral unmixing, and graph signal recovery.

Graph Spatio-Spectral Total Variation Model for Hyperspectral Image Denoising

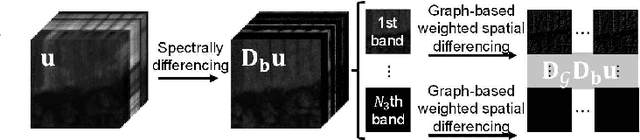
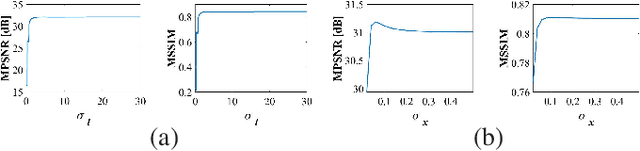
The spatio-spectral total variation (SSTV) model has been widely used as an effective regularization of hyperspectral images (HSI) for various applications such as mixed noise removal. However, since SSTV computes local spatial differences uniformly, it is difficult to remove noise while preserving complex spatial structures with fine edges and textures, especially in situations of high noise intensity. To solve this problem, we propose a new TV-type regularization called Graph-SSTV (GSSTV), which generates a graph explicitly reflecting the spatial structure of the target HSI from noisy HSIs and incorporates a weighted spatial difference operator designed based on this graph. Furthermore, we formulate the mixed noise removal problem as a convex optimization problem involving GSSTV and develop an efficient algorithm based on the primal-dual splitting method to solve this problem. Finally, we demonstrate the effectiveness of GSSTV compared with existing HSI regularization models through experiments on mixed noise removal. The source code will be available at https://www.mdi.c.titech.ac.jp/publications/gsstv.

Zero-Gradient Constrained Optimization for Destriping of 3D Imaging Data

This paper proposes an effective and efficient destriping method based on zero-gradient constraints, which are compatible with various regularization functions. Removing stripe noise, i.e., destriping, from three-dimensional (3D) imaging data is an essential task in terms of visual quality and subsequent processing. Stripe noise has flat structures in the vertical and temporal directions, meaning that the vertical and temporal gradients are equal to zero. Exploiting this fact, we first propose a new model for characterizing stripe noise. Our model constrains the stripe noise gradient to be zero, which we name the zero-gradient constraint, leading to effective destriping regardless of what regularization is applied to imaging data. Then, we formulate two types of convex optimization problems involving the zero-gradient constraints for destriping and develop efficient solvers for the problems based on a diagonally preconditioned primal-dual splitting algorithm (DP-PDS). We demonstrate the advantages of our model through destriping experiments using hyperspectral images (HSI) and infrared (IR) videos.