Geometric Spatio-Spectral Total Variation for Hyperspectral Image Denoising and Destriping

This article proposes a novel regularization method, named Geometric Spatio-Spectral Total Variation (GeoSSTV), for hyperspectral (HS) image denoising and destriping. HS images are inevitably affected by various types of noise due to the measurement equipment and environment. Total Variation (TV)-based regularization methods that model the spatio-spectral piecewise smoothness inherent in HS images are promising approaches for HS image denoising and destriping. However, existing TV-based methods are based on classical anisotropic and isotropic TVs, which cause staircase artifacts and lack rotation invariance, respectively, making it difficult to accurately recover round structures and oblique edges. To address this issue, GeoSSTV introduces a geometrically consistent formulation of TV that measures variations across all directions in a Euclidean manner. Through this formulation, GeoSSTV removes noise while preserving round structures and oblique edges. Furthermore, we formulate the HS image denoising problem as a constrained convex optimization problem involving GeoSSTV and develop an efficient algorithm based on a preconditioned primal-dual splitting method. Experimental results on HS images contaminated with mixed noise demonstrate the superiority of the proposed method over existing approaches.

Efficient and Accurate Full-Waveform Inversion with Total Variation Constraint

This paper proposes a computationally efficient algorithm to address the Full-Waveform Inversion (FWI) problem with a Total Variation (TV) constraint, designed to accurately reconstruct subsurface properties from seismic data. FWI, as an ill-posed inverse problem, requires effective regularizations or constraints to ensure accurate and stable solutions. Among these, the TV constraint is widely known as a powerful prior for modeling the piecewise smooth structure of subsurface properties. However, solving the optimization problem is challenging because of the nonlinear observation process combined with the non-smoothness of the TV constraint. Conventional methods rely on inner loops and/or approximations, which lead to high computational cost and/or inappropriate solutions. To address these limitations, we develop a novel algorithm based on a primal-dual splitting method, achieving computational efficiency by eliminating inner loops and ensuring high accuracy by avoiding approximations. We also demonstrate the effectiveness of the proposed method through experiments using the SEG/EAGE Salt and Overthrust Models. The source code will be available at https://www.mdi.c.titech.ac.jp/publications/fwiwtv.

Spatio-Spectral Structure Tensor Total Variation for Hyperspectral Image Denoising and Destriping

This paper proposes a novel regularization method, named Spatio-Spectral Structure Tensor Total Variation (S3TTV), for denoising and destriping of hyperspectral (HS) images. HS images are inevitably contaminated by various types of noise, during acquisition process, due to the measurement equipment and the environment. For HS image denoising and destriping tasks, Spatio-Spectral Total Variation (SSTV), defined using second-order spatio-spectral differences, is widely known as a powerful regularization approach that models the underlying spatio-spectral properties. However, since SSTV refers only to adjacent pixels/bands, semi-local spatial structures are not preserved during denoising process. To address this problem, we newly design S3TTV, defined by the sum of the nuclear norms of matrices consisting of second-order spatio-spectral differences in small spectral blocks (we call these matrices as spatio-spectral structure tensors). The proposed regularization method simultaneously models the spatial piecewise-smoothness, the spatial similarity between adjacent bands, and the spectral correlation across all bands in small spectral blocks, leading to effective noise removal while preserving the semi-local spatial structures. Furthermore, we formulate the HS image denoising and destriping problem as a convex optimization problem involving S3TTV and develop an algorithm based on a preconditioned primal-dual splitting method to solve this problem efficiently. Finally, we demonstrate the effectiveness of S3TTV by comparing it with existing methods, including state-of-the-art ones through denoising and destriping experiments.

Graph Spatio-Spectral Total Variation Model for Hyperspectral Image Denoising

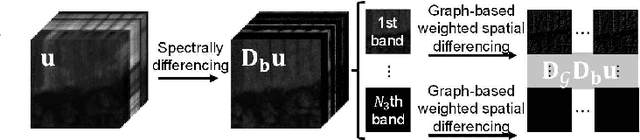
The spatio-spectral total variation (SSTV) model has been widely used as an effective regularization of hyperspectral images (HSI) for various applications such as mixed noise removal. However, since SSTV computes local spatial differences uniformly, it is difficult to remove noise while preserving complex spatial structures with fine edges and textures, especially in situations of high noise intensity. To solve this problem, we propose a new TV-type regularization called Graph-SSTV (GSSTV), which generates a graph explicitly reflecting the spatial structure of the target HSI from noisy HSIs and incorporates a weighted spatial difference operator designed based on this graph. Furthermore, we formulate the mixed noise removal problem as a convex optimization problem involving GSSTV and develop an efficient algorithm based on the primal-dual splitting method to solve this problem. Finally, we demonstrate the effectiveness of GSSTV compared with existing HSI regularization models through experiments on mixed noise removal. The source code will be available at https://www.mdi.c.titech.ac.jp/publications/gsstv.