Sampling Method for Generalized Graph Signals with Pre-selected Vertices via DC Optimization

This paper proposes a method for vertex-wise flexible sampling of a broad class of graph signals, designed to attain the best possible recovery based on the generalized sampling theory. This is achieved by designing a sampling operator by an optimization problem, which is inherently non-convex, as the best possible recovery imposes a rank constraint. An existing method for vertex-wise flexible sampling is able to control the number of active vertices but cannot incorporate prior knowledge of mandatory or forbidden vertices. To address these challenges, we formulate the operator design as a problem that handles a constraint of the number of active vertices and prior knowledge on specific vertices for sampling, mandatory inclusion or exclusion. We transformed this constrained problem into a difference-of-convex (DC) optimization problem by using the nuclear norm and a DC penalty for vertex selection. To solve this, we develop a convergent solver based on the general double-proximal gradient DC algorithm. The effectiveness of our method is demonstrated through experiments on various graph signal models, including real-world data, showing superior performance in the recovery accuracy by comparing to existing methods.

Graph Signal Sampling Under Smoothness Priors: A Difference-of-Convex Approach

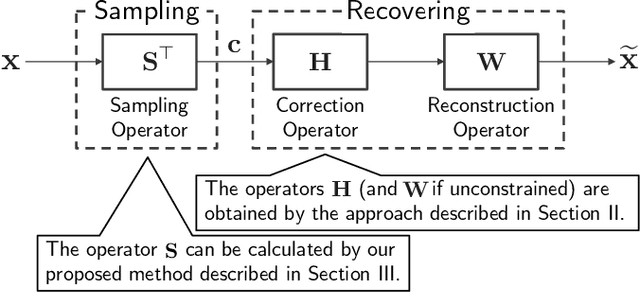
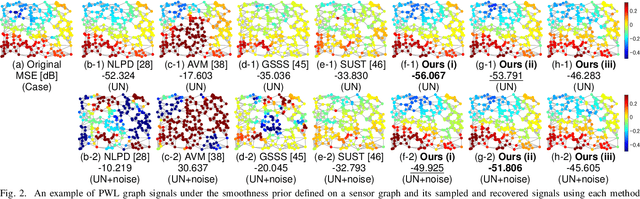
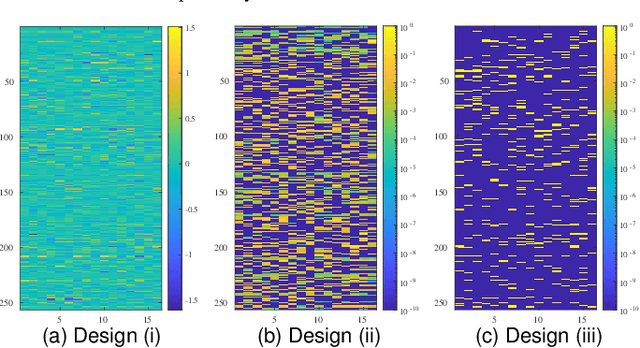
This paper proposes a method for properly sampling graph signals under smoothness priors. Unlike many existing approaches that assume bandlimited graph signals, our method designs a sampling operator for graph signals that are not necessarily bandlimited based on the generalized sampling theory. First, we formulate the sampling operator design under smoothness priors as a feasibility problem. Then, we transform this problem into a Difference-of-Convex (DC) problem by relaxing a certain invertibility constraint in the original problem using the nuclear norm. Furthermore, we develop an efficient algorithm to solve this DC problem based on the proximal linearized difference-of-convex algorithm and guarantee its convergence to a critical point of the problem. Finally, we demonstrate the effectiveness of our method for several graph signal models through sampling-and-reconstruction experiments.