Physics-informed neural networks need a physicist to be accurate: the case of mass and heat transport in Fischer-Tropsch catalyst particles

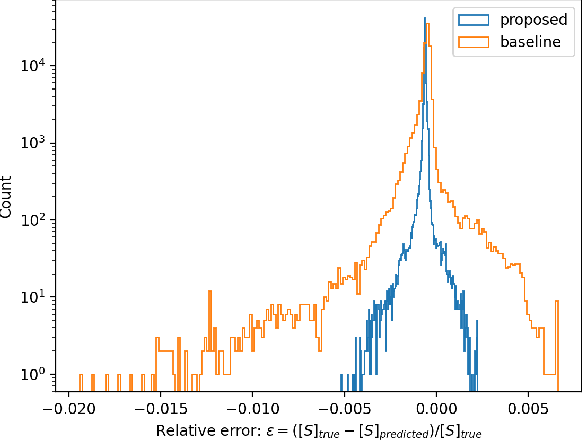
Physics-Informed Neural Networks (PINNs) have emerged as an influential technology, merging the swift and automated capabilities of machine learning with the precision and dependability of simulations grounded in theoretical physics. PINNs are often employed to solve algebraic or differential equations to replace some or even all steps of multi-stage computational workflows, leading to their significant speed-up. However, wide adoption of PINNs is still hindered by reliability issues, particularly at extreme ends of the input parameter ranges. In this study, we demonstrate this in the context of a system of coupled non-linear differential reaction-diffusion and heat transfer equations related to Fischer-Tropsch synthesis, which are solved by a finite-difference method with a PINN used in evaluating their source terms. It is shown that the testing strategies traditionally used to assess the accuracy of neural networks as function approximators can overlook the peculiarities which ultimately cause instabilities of the finite-difference solver. We propose a domain knowledge-based modifications to the PINN architecture ensuring its correct asymptotic behavior. When combined with an improved numerical scheme employed as an initial guess generator, the proposed modifications are shown to recover the overall stability of the simulations, while preserving the speed-up brought by PINN as the workflow component. We discuss the possible applications of the proposed hybrid transport equation solver in context of chemical reactors simulations.

Large Language Model-Based Evolutionary Optimizer: Reasoning with elitism

Large Language Models (LLMs) have demonstrated remarkable reasoning abilities, prompting interest in their application as black-box optimizers. This paper asserts that LLMs possess the capability for zero-shot optimization across diverse scenarios, including multi-objective and high-dimensional problems. We introduce a novel population-based method for numerical optimization using LLMs called Language-Model-Based Evolutionary Optimizer (LEO). Our hypothesis is supported through numerical examples, spanning benchmark and industrial engineering problems such as supersonic nozzle shape optimization, heat transfer, and windfarm layout optimization. We compare our method to several gradient-based and gradient-free optimization approaches. While LLMs yield comparable results to state-of-the-art methods, their imaginative nature and propensity to hallucinate demand careful handling. We provide practical guidelines for obtaining reliable answers from LLMs and discuss method limitations and potential research directions.

Accurate and Fast Fischer-Tropsch Reaction Microkinetics using PINNs

Microkinetics allows detailed modelling of chemical transformations occurring in many industrially relevant reactions. Traditional way of solving the microkinetics model for Fischer-Tropsch synthesis (FTS) becomes inefficient when it comes to more advanced real-time applications. In this work, we address these challenges by using physics-informed neural networks(PINNs) for modelling FTS microkinetics. We propose a computationally efficient and accurate method, enabling the ultra-fast solution of the existing microkinetics models in realistic process conditions. The proposed PINN model computes the fraction of vacant catalytic sites, a key quantity in FTS microkinetics, with median relative error (MRE) of 0.03%, and the FTS product formation rates with MRE of 0.1%. Compared to conventional equation solvers, the model achieves up to 1E+06 times speed-up when running on GPUs, thus being fast enough for multi-scale and multi-physics reactor modelling and enabling its applications in real-time process control and optimization.