Bayesian Numerical Integration with Neural Networks

Bayesian probabilistic numerical methods for numerical integration offer significant advantages over their non-Bayesian counterparts: they can encode prior information about the integrand, and can quantify uncertainty over estimates of an integral. However, the most popular algorithm in this class, Bayesian quadrature, is based on Gaussian process models and is therefore associated with a high computational cost. To improve scalability, we propose an alternative approach based on Bayesian neural networks which we call Bayesian Stein networks. The key ingredients are a neural network architecture based on Stein operators, and an approximation of the Bayesian posterior based on the Laplace approximation. We show that this leads to orders of magnitude speed-ups on the popular Genz functions benchmark, and on challenging problems arising in the Bayesian analysis of dynamical systems, and the prediction of energy production for a large-scale wind farm.

Uncertainty and Structure in Neural Ordinary Differential Equations

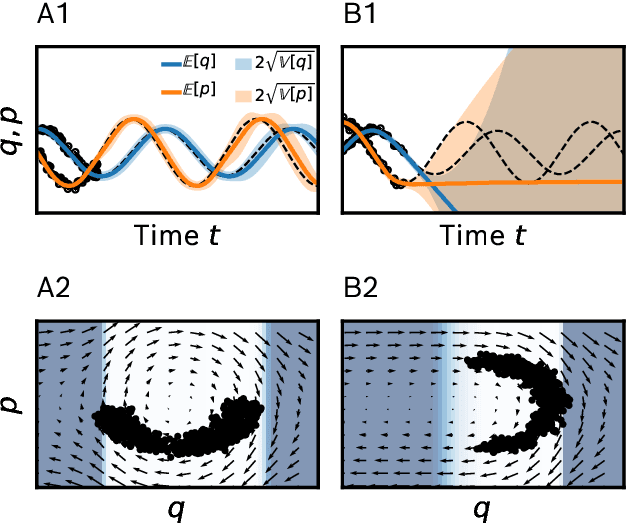
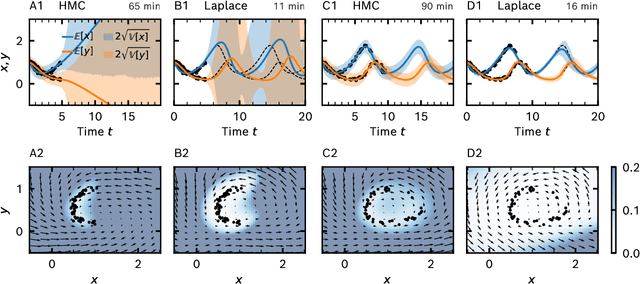
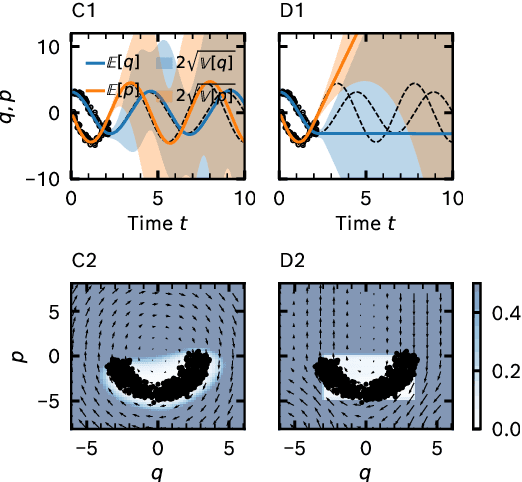
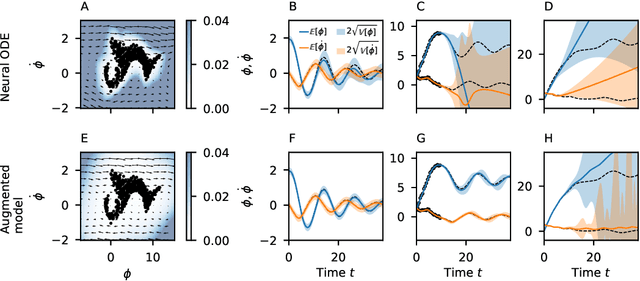
Neural ordinary differential equations (ODEs) are an emerging class of deep learning models for dynamical systems. They are particularly useful for learning an ODE vector field from observed trajectories (i.e., inverse problems). We here consider aspects of these models relevant for their application in science and engineering. Scientific predictions generally require structured uncertainty estimates. As a first contribution, we show that basic and lightweight Bayesian deep learning techniques like the Laplace approximation can be applied to neural ODEs to yield structured and meaningful uncertainty quantification. But, in the scientific domain, available information often goes beyond raw trajectories, and also includes mechanistic knowledge, e.g., in the form of conservation laws. We explore how mechanistic knowledge and uncertainty quantification interact on two recently proposed neural ODE frameworks - symplectic neural ODEs and physical models augmented with neural ODEs. In particular, uncertainty reflects the effect of mechanistic information more directly than the predictive power of the trained model could. And vice versa, structure can improve the extrapolation abilities of neural ODEs, a fact that can be best assessed in practice through uncertainty estimates. Our experimental analysis demonstrates the effectiveness of the Laplace approach on both low dimensional ODE problems and a high dimensional partial differential equation.

When are Neural ODE Solutions Proper ODEs?

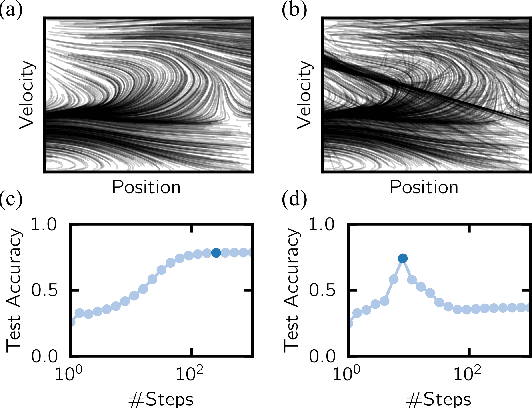
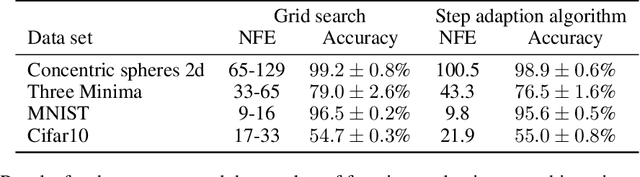
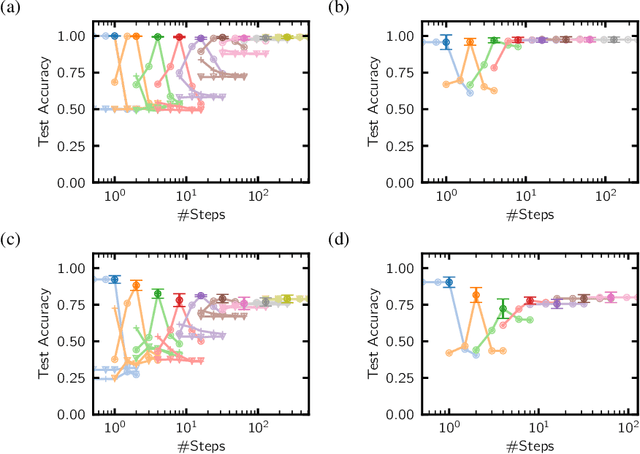
A key appeal of the recently proposed Neural Ordinary Differential Equation(ODE) framework is that it seems to provide a continuous-time extension of discrete residual neural networks. As we show herein, though, trained Neural ODE models actually depend on the specific numerical method used during training. If the trained model is supposed to be a flow generated from an ODE, it should be possible to choose another numerical solver with equal or smaller numerical error without loss of performance. We observe that if training relies on a solver with overly coarse discretization, then testing with another solver of equal or smaller numerical error results in a sharp drop in accuracy. In such cases, the combination of vector field and numerical method cannot be interpreted as a flow generated from an ODE, which arguably poses a fatal breakdown of the Neural ODE concept. We observe, however, that there exists a critical step size beyond which the training yields a valid ODE vector field. We propose a method that monitors the behavior of the ODE solver during training to adapt its step size, aiming to ensure a valid ODE without unnecessarily increasing computational cost. We verify this adaption algorithm on two common bench mark datasets as well as a synthetic dataset. Furthermore, we introduce a novel synthetic dataset in which the underlying ODE directly generates a classification task.