Motif Discovery Framework for Psychiatric EEG Data Classification

In current medical practice, patients undergoing depression treatment must wait four to six weeks before a clinician can assess medication response due to the delayed noticeable effects of antidepressants. Identification of a treatment response at any earlier stage is of great importance, since it can reduce the emotional and economic burden connected with the treatment. We approach the prediction of a patient response to a treatment as a classification problem, by utilizing the dynamic properties of EEG recordings on the 7th day of the treatment. We present a novel framework that applies motif discovery to extract meaningful features from EEG data distinguishing between depression treatment responders and non-responders. We applied our framework also to classification tasks in other psychiatric EEG datasets, namely to patients with symptoms of schizophrenia, pediatric patients with intractable seizures, and Alzheimer disease and dementia. We achieved high classification precision in all data sets. The results demonstrate that the dynamic properties of the EEGs may support clinicians in decision making both in diagnosis and in the prediction depression treatment response as early as on the 7th day of the treatment. To our best knowledge, our work is the first one using motifs in the depression diagnostics in general.

Granger Causal Inference in Multivariate Hawkes Processes by Minimum Message Length

Multivariate Hawkes processes (MHPs) are versatile probabilistic tools used to model various real-life phenomena: earthquakes, operations on stock markets, neuronal activity, virus propagation and many others. In this paper, we focus on MHPs with exponential decay kernels and estimate connectivity graphs, which represent the Granger causal relations between their components. We approach this inference problem by proposing an optimization criterion and model selection algorithm based on the minimum message length (MML) principle. MML compares Granger causal models using the Occam's razor principle in the following way: even when models have a comparable goodness-of-fit to the observed data, the one generating the most concise explanation of the data is preferred. While most of the state-of-art methods using lasso-type penalization tend to overfitting in scenarios with short time horizons, the proposed MML-based method achieves high F1 scores in these settings. We conduct a numerical study comparing the proposed algorithm to other related classical and state-of-art methods, where we achieve the highest F1 scores in specific sparse graph settings. We illustrate the proposed method also on G7 sovereign bond data and obtain causal connections, which are in agreement with the expert knowledge available in the literature.

AWT -- Clustering Meteorological Time Series Using an Aggregated Wavelet Tree

Both clustering and outlier detection play an important role for meteorological measurements. We present the AWT algorithm, a clustering algorithm for time series data that also performs implicit outlier detection during the clustering. AWT integrates ideas of several well-known K-Means clustering algorithms. It chooses the number of clusters automatically based on a user-defined threshold parameter, and it can be used for heterogeneous meteorological input data as well as for data sets that exceed the available memory size. We apply AWT to crowd sourced 2-m temperature data with an hourly resolution from the city of Vienna to detect outliers and to investigate if the final clusters show general similarities and similarities with urban land-use characteristics. It is shown that both the outlier detection and the implicit mapping to land-use characteristic is possible with AWT which opens new possible fields of application, specifically in the rapidly evolving field of urban climate and urban weather.

Interpretable Gait Recognition by Granger Causality

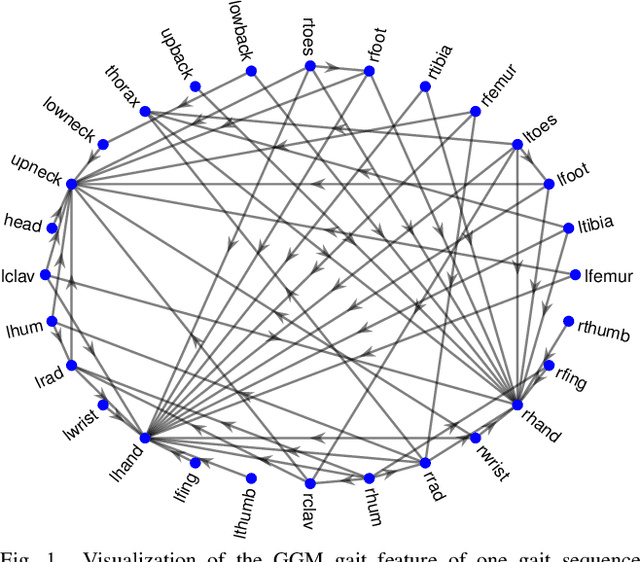
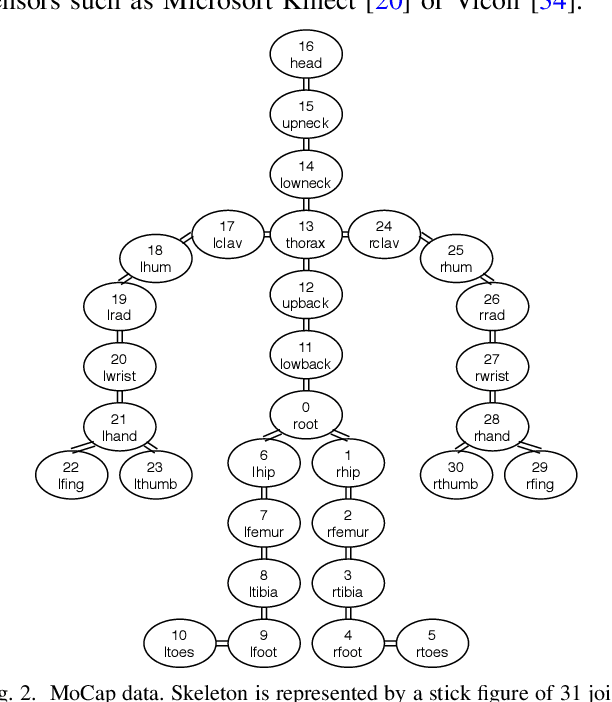
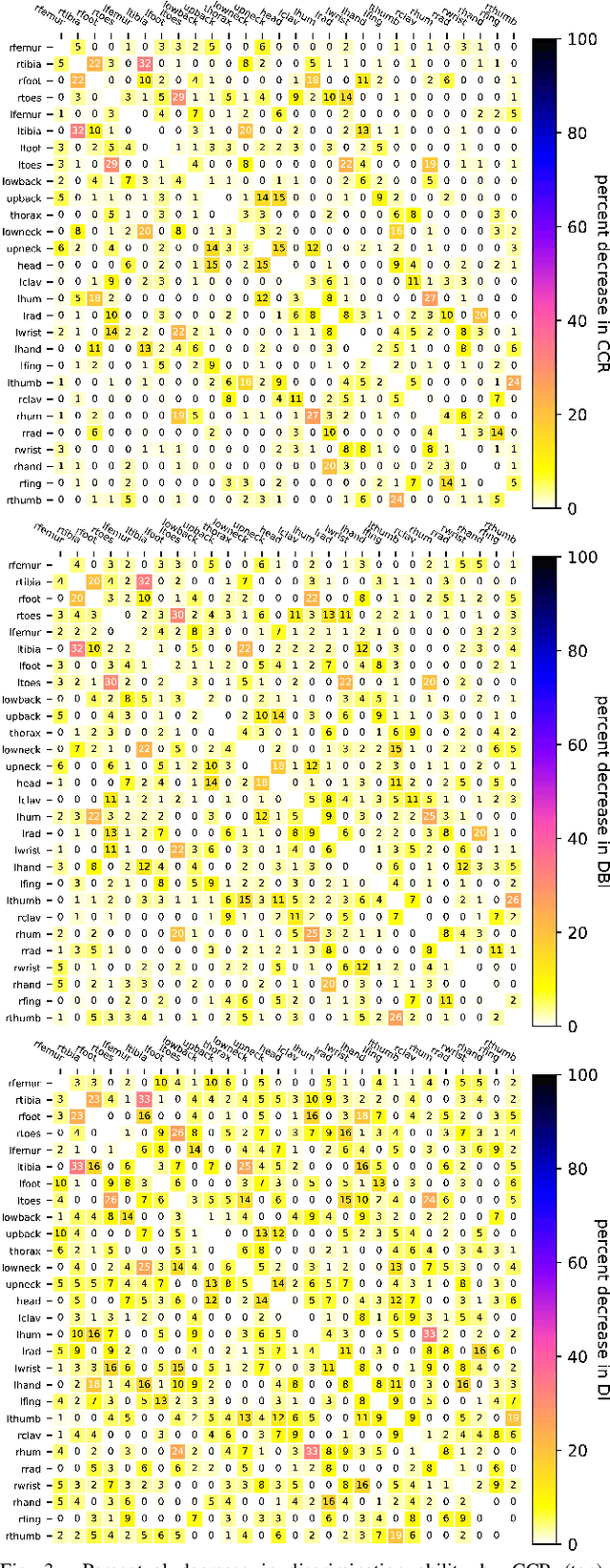
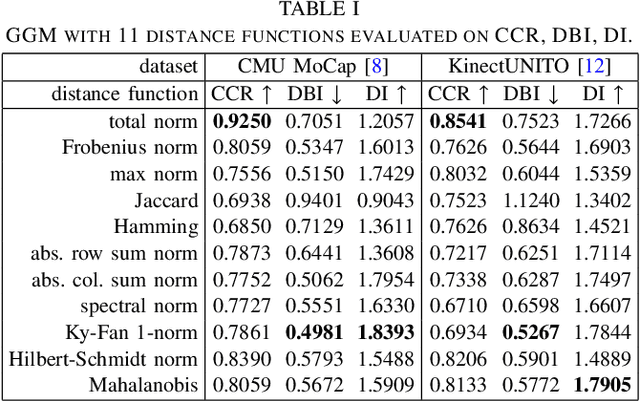
Which joint interactions in the human gait cycle can be used as biometric characteristics? Most current methods on gait recognition suffer from the lack of interpretability. We propose an interpretable feature representation of gait sequences by the graphical Granger causal inference. Gait sequence of a person in the standardized motion capture format, constituting a set of 3D joint spatial trajectories, is envisaged as a causal system of joints interacting in time. We apply the graphical Granger model (GGM) to obtain the so-called Granger causal graph among joints as a discriminative and visually interpretable representation of a person's gait. We evaluate eleven distance functions in the GGM feature space by established classification and class-separability evaluation metrics. Our experiments indicate that, depending on the metric, the most appropriate distance functions for the GGM are the total norm distance and the Ky-Fan 1-norm distance. Experiments also show that the GGM is able to detect the most discriminative joint interactions and that it outperforms five related interpretable models in correct classification rate and in Davies-Bouldin index. The proposed GGM model can serve as a complementary tool for gait analysis in kinesiology or for gait recognition in video surveillance.

Causal Discovery in Hawkes Processes by Minimum Description Length

Hawkes processes are a special class of temporal point processes which exhibit a natural notion of causality, as occurrence of events in the past may increase the probability of events in the future. Discovery of the underlying influence network among the dimensions of multi-dimensional temporal processes is of high importance in disciplines where a high-frequency data is to model, e.g. in financial data or in seismological data. This paper approaches the problem of learning Granger-causal network in multi-dimensional Hawkes processes. We formulate this problem as a model selection task in which we follow the minimum description length (MDL) principle. Moreover, we propose a general algorithm for MDL-based inference using a Monte-Carlo method and we use it for our causal discovery problem. We compare our algorithm with the state-of-the-art baseline methods on synthetic and real-world financial data. The synthetic experiments demonstrate superiority of our method incausal graph discovery compared to the baseline methods with respect to the size of the data. The results of experiments with the G-7 bonds price data are consistent with the experts knowledge.