On the Theory of Stochastic Automata

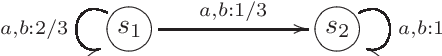
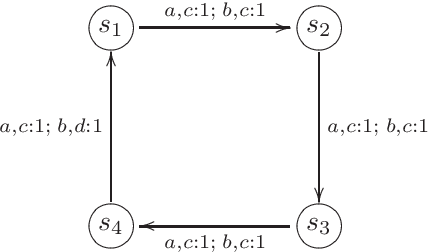
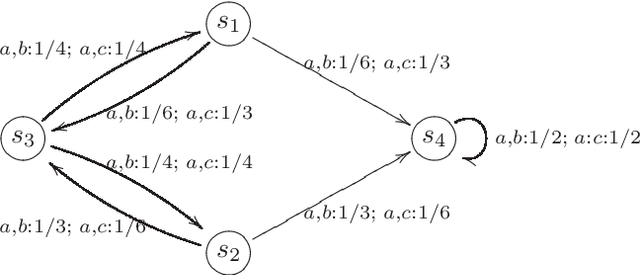
The theory of discrete stochastic systems has been initiated by the work of Shannon and von Neumann. While Shannon has considered memory-less communication channels and their generalization by introducing states, von Neumann has studied the synthesis of reliable systems from unreliable components. The fundamental work of Rabin and Scott about deterministic finite-state automata has led to two generalizations. First, the generalization of transition functions to conditional distributions studied by Carlyle and Starke. This in turn has led to a generalization of time-discrete Markov chains in which the chains are governed by more than one transition probability matrix. Second, the generalization of regular sets by introducing stochastic automata as described by Rabin. Stochastic automata are well-investigated. This report provides a short introduction to stochastic automata based on the valuable book of Claus. This includes the basic topics of the theory of stochastic automata: equivalence, minimization, reduction, covering, observability, and determinism. Then stochastic versions of Mealy and Moore automata are studied and finally stochastic language acceptors are considered as a generalization of nondeterministic finite-state acceptors.

On the decomposition of generalized semiautomata

Semi-automata are abstractions of electronic devices that are deterministic finite-state machines having inputs but no outputs. Generalized semiautomata are obtained from stochastic semiautomata by dropping the restrictions imposed by probability. It is well-known that each stochastic semiautomaton can be decomposed into a sequential product of a dependent source and a deterministic semiautomaton making partly use of the celebrated theorem of Birkhoff-von Neumann. It will be shown that each generalized semiautomaton can be partitioned into a sequential product of a generalized dependent source and a deterministic semiautomaton.

On Stochastic Automata over Monoids

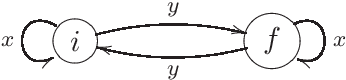
Stochastic automata over monoids as input sets are studied. The well-definedness of these automata requires an extension postulate that replaces the inherent universal property of free monoids. As a generalization of Turakainen's result, it will be shown that the generalized automata over monoids have the same acceptance power as their stochastic counterparts. The key to homomorphisms is a commuting property between the monoid homomorphism of input states and the monoid homomorphism of transition matrices. Closure properties of the languages accepted by stochastic automata over monoids are investigated. matrices. Closure properties of the languages accepted by stochastic automata over monoids are investigated.

Inference in Graded Bayesian Networks

Machine learning provides algorithms that can learn from data and make inferences or predictions on data. Bayesian networks are a class of graphical models that allow to represent a collection of random variables and their condititional dependencies by directed acyclic graphs. In this paper, an inference algorithm for the hidden random variables of a Bayesian network is given by using the tropicalization of the marginal distribution of the observed variables. By restricting the topological structure to graded networks, an inference algorithm for graded Bayesian networks will be established that evaluates the hidden random variables rank by rank and in this way yields the most probable states of the hidden variables. This algorithm can be viewed as a generalized version of the Viterbi algorithm for graded Bayesian networks.

Computations in Stochastic Acceptors

Machine learning provides algorithms that can learn from data and make inferences or predictions on data. Stochastic acceptors or probabilistic automata are stochastic automata without output that can model components in machine learning scenarios. In this paper, we provide dynamic programming algorithms for the computation of input marginals and the acceptance probabilities in stochastic acceptors. Furthermore, we specify an algorithm for the parameter estimation of the conditional probabilities using the expectation-maximization technique and a more efficient implementation related to the Baum-Welch algorithm.

D-Bees: A Novel Method Inspired by Bee Colony Optimization for Solving Word Sense Disambiguation

Word sense disambiguation (WSD) is a problem in the field of computational linguistics given as finding the intended sense of a word (or a set of words) when it is activated within a certain context. WSD was recently addressed as a combinatorial optimization problem in which the goal is to find a sequence of senses that maximize the semantic relatedness among the target words. In this article, a novel algorithm for solving the WSD problem called D-Bees is proposed which is inspired by bee colony optimization (BCO)where artificial bee agents collaborate to solve the problem. The D-Bees algorithm is evaluated on a standard dataset (SemEval 2007 coarse-grained English all-words task corpus)and is compared to simulated annealing, genetic algorithms, and two ant colony optimization techniques (ACO). It will be observed that the BCO and ACO approaches are on par.