On the Theory of Stochastic Automata
Paper and Code
Mar 26, 2021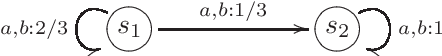

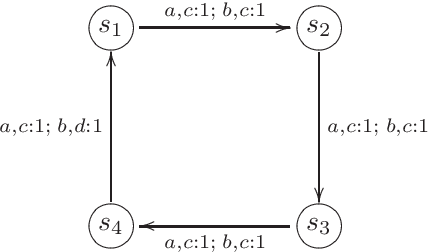
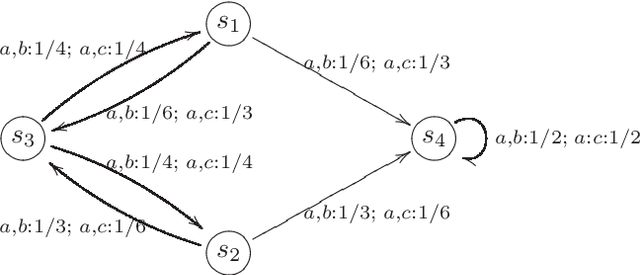
The theory of discrete stochastic systems has been initiated by the work of Shannon and von Neumann. While Shannon has considered memory-less communication channels and their generalization by introducing states, von Neumann has studied the synthesis of reliable systems from unreliable components. The fundamental work of Rabin and Scott about deterministic finite-state automata has led to two generalizations. First, the generalization of transition functions to conditional distributions studied by Carlyle and Starke. This in turn has led to a generalization of time-discrete Markov chains in which the chains are governed by more than one transition probability matrix. Second, the generalization of regular sets by introducing stochastic automata as described by Rabin. Stochastic automata are well-investigated. This report provides a short introduction to stochastic automata based on the valuable book of Claus. This includes the basic topics of the theory of stochastic automata: equivalence, minimization, reduction, covering, observability, and determinism. Then stochastic versions of Mealy and Moore automata are studied and finally stochastic language acceptors are considered as a generalization of nondeterministic finite-state acceptors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge