Merve Nur Cakir
On the Theory of Stochastic Automata
Mar 26, 2021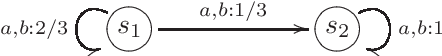

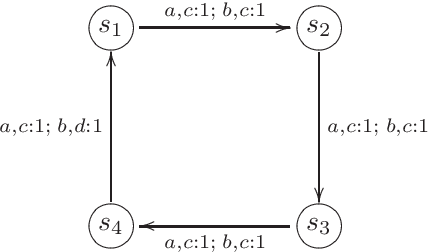
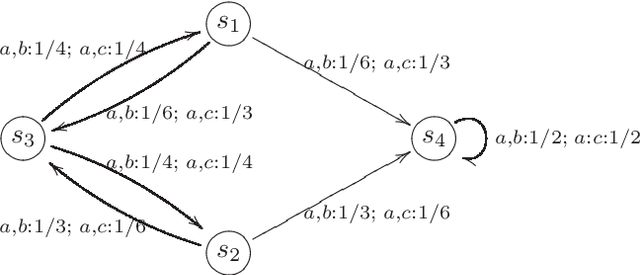
Abstract:The theory of discrete stochastic systems has been initiated by the work of Shannon and von Neumann. While Shannon has considered memory-less communication channels and their generalization by introducing states, von Neumann has studied the synthesis of reliable systems from unreliable components. The fundamental work of Rabin and Scott about deterministic finite-state automata has led to two generalizations. First, the generalization of transition functions to conditional distributions studied by Carlyle and Starke. This in turn has led to a generalization of time-discrete Markov chains in which the chains are governed by more than one transition probability matrix. Second, the generalization of regular sets by introducing stochastic automata as described by Rabin. Stochastic automata are well-investigated. This report provides a short introduction to stochastic automata based on the valuable book of Claus. This includes the basic topics of the theory of stochastic automata: equivalence, minimization, reduction, covering, observability, and determinism. Then stochastic versions of Mealy and Moore automata are studied and finally stochastic language acceptors are considered as a generalization of nondeterministic finite-state acceptors.
On the decomposition of generalized semiautomata
Apr 19, 2020
Abstract:Semi-automata are abstractions of electronic devices that are deterministic finite-state machines having inputs but no outputs. Generalized semiautomata are obtained from stochastic semiautomata by dropping the restrictions imposed by probability. It is well-known that each stochastic semiautomaton can be decomposed into a sequential product of a dependent source and a deterministic semiautomaton making partly use of the celebrated theorem of Birkhoff-von Neumann. It will be shown that each generalized semiautomaton can be partitioned into a sequential product of a generalized dependent source and a deterministic semiautomaton.
On Stochastic Automata over Monoids
Feb 04, 2020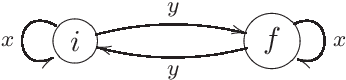

Abstract:Stochastic automata over monoids as input sets are studied. The well-definedness of these automata requires an extension postulate that replaces the inherent universal property of free monoids. As a generalization of Turakainen's result, it will be shown that the generalized automata over monoids have the same acceptance power as their stochastic counterparts. The key to homomorphisms is a commuting property between the monoid homomorphism of input states and the monoid homomorphism of transition matrices. Closure properties of the languages accepted by stochastic automata over monoids are investigated. matrices. Closure properties of the languages accepted by stochastic automata over monoids are investigated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge