Exploratory Factor Analysis of Data on a Sphere

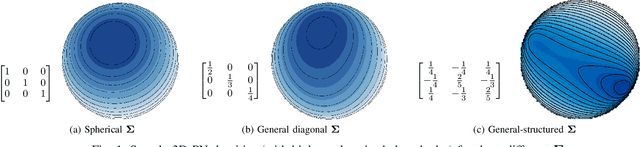
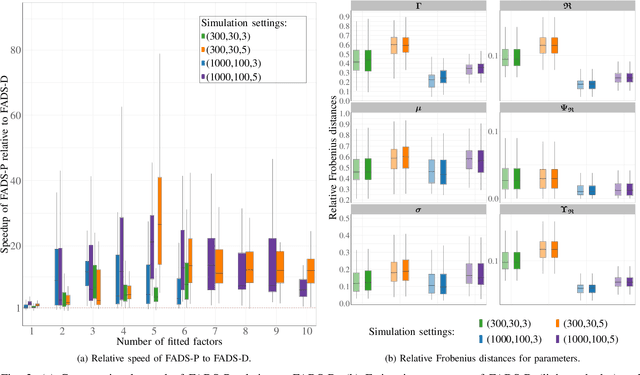
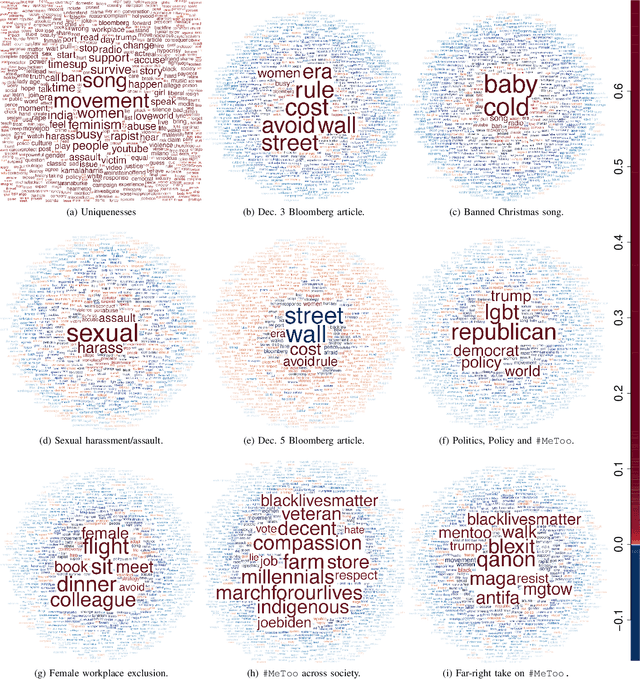
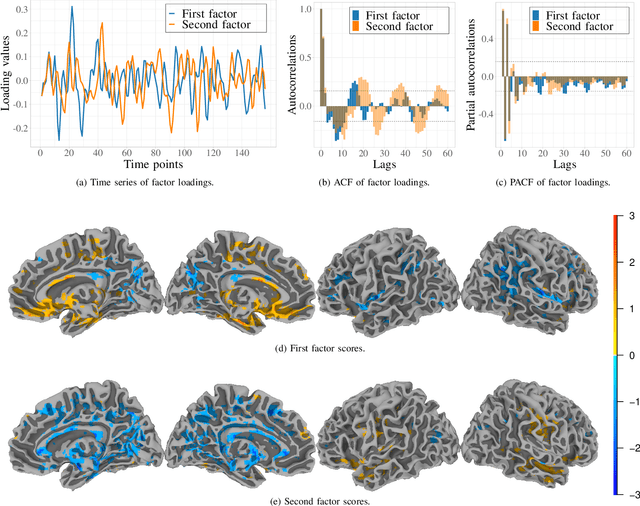
Data on high-dimensional spheres arise frequently in many disciplines either naturally or as a consequence of preliminary processing and can have intricate dependence structure that needs to be understood. We develop exploratory factor analysis of the projected normal distribution to explain the variability in such data using a few easily interpreted latent factors. Our methodology provides maximum likelihood estimates through a novel fast alternating expectation profile conditional maximization algorithm. Results on simulation experiments on a wide range of settings are uniformly excellent. Our methodology provides interpretable and insightful results when applied to tweets with the $\#MeToo$ hashtag in early December 2018, to time-course functional Magnetic Resonance Images of the average pre-teen brain at rest, to characterize handwritten digits, and to gene expression data from cancerous cells in the Cancer Genome Atlas.

An Efficient $k$-modes Algorithm for Clustering Categorical Datasets

Mining clusters from datasets is an important endeavor in many applications. The $k$-means algorithm is a popular and efficient distribution-free approach for clustering numerical-valued data but can not be applied to categorical-valued observations. The $k$-modes algorithm addresses this lacuna by taking the $k$-means objective function, replacing the dissimilarity measure and using modes instead of means in the modified objective function. Unlike many other clustering algorithms, both $k$-modes and $k$-means are scalable, because they do not require calculation of all pairwise dissimilarities. We provide a fast and computationally efficient implementation of $k$-modes, OTQT, and prove that it can find superior clusterings to existing algorithms. We also examine five initialization methods and three types of $K$-selection methods, many of them novel, and all appropriate for $k$-modes. By examining the performance on real and simulated datasets, we show that simple random initialization is the best intializer, a novel $K$-selection method is more accurate than two methods adapted from $k$-means, and that the new OTQT algorithm is more accurate and almost always faster than existing algorithms.