Kangbo Hao
Precision annealing Monte Carlo methods for statistical data assimilation and machine learning
Jul 06, 2019
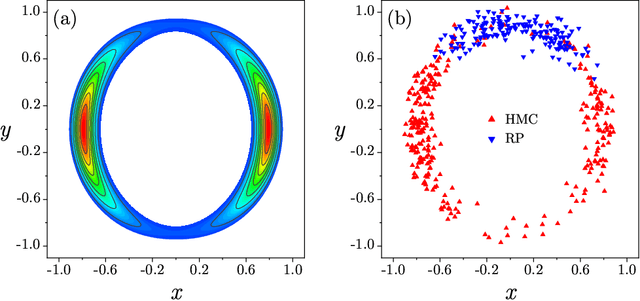

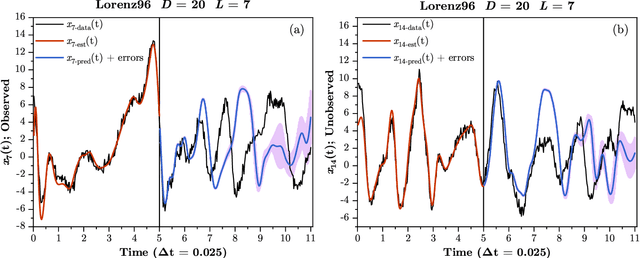
Abstract:In statistical data assimilation (SDA) and supervised machine learning (ML), we wish to transfer information from observations to a model of the processes underlying those observations. For SDA, the model consists of a set of differential equations that describe the dynamics of a physical system. For ML, the model is usually constructed using other strategies. In this paper, we develop a systematic formulation based on Monte Carlo sampling to achieve such information transfer. Following the derivation of an appropriate target distribution, we present the formulation based on the standard Metropolis-Hasting (MH) procedure and the Hamiltonian Monte Carlo (HMC) method for performing the high dimensional integrals that appear. To the extensive literature on MH and HMC, we add (1) an annealing method using a hyperparameter that governs the precision of the model to identify and explore the highest probability regions of phase space dominating those integrals, and (2) a strategy for initializing the state space search. The efficacy of the proposed formulation is demonstrated using a nonlinear dynamical model with chaotic solutions widely used in geophysics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge