Max-Margin Feature Selection

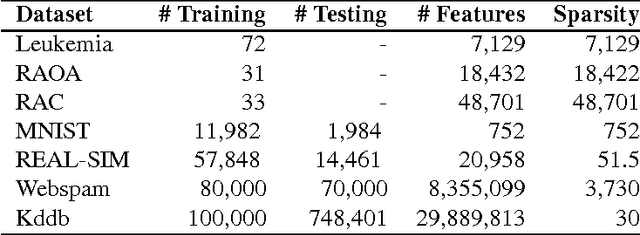
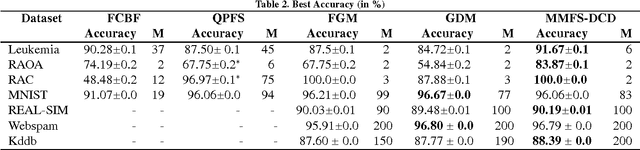
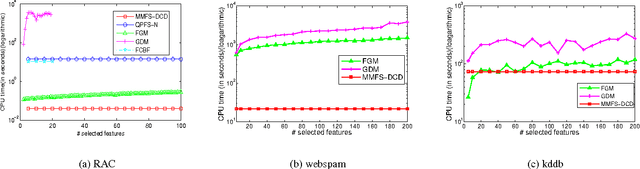
Many machine learning applications such as in vision, biology and social networking deal with data in high dimensions. Feature selection is typically employed to select a subset of features which im- proves generalization accuracy as well as reduces the computational cost of learning the model. One of the criteria used for feature selection is to jointly minimize the redundancy and maximize the rele- vance of the selected features. In this paper, we formulate the task of feature selection as a one class SVM problem in a space where features correspond to the data points and instances correspond to the dimensions. The goal is to look for a representative subset of the features (support vectors) which describes the boundary for the region where the set of the features (data points) exists. This leads to a joint optimization of relevance and redundancy in a principled max-margin framework. Additionally, our formulation enables us to leverage existing techniques for optimizing the SVM objective resulting in highly computationally efficient solutions for the task of feature selection. Specifically, we employ the dual coordinate descent algorithm (Hsieh et al., 2008), originally proposed for SVMs, for our formulation. We use a sparse representation to deal with data in very high dimensions. Experiments on seven publicly available benchmark datasets from a variety of domains show that our approach results in orders of magnitude faster solutions even while retaining the same level of accuracy compared to the state of the art feature selection techniques.

Integrating K-means with Quadratic Programming Feature Selection

Several data mining problems are characterized by data in high dimensions. One of the popular ways to reduce the dimensionality of the data is to perform feature selection, i.e, select a subset of relevant and non-redundant features. Recently, Quadratic Programming Feature Selection (QPFS) has been proposed which formulates the feature selection problem as a quadratic program. It has been shown to outperform many of the existing feature selection methods for a variety of applications. Though, better than many existing approaches, the running time complexity of QPFS is cubic in the number of features, which can be quite computationally expensive even for moderately sized datasets. In this paper we propose a novel method for feature selection by integrating k-means clustering with QPFS. The basic variant of our approach runs k-means to bring down the number of features which need to be passed on to QPFS. We then enhance this idea, wherein we gradually refine the feature space from a very coarse clustering to a fine-grained one, by interleaving steps of QPFS with k-means clustering. Every step of QPFS helps in identifying the clusters of irrelevant features (which can then be thrown away), whereas every step of k-means further refines the clusters which are potentially relevant. We show that our iterative refinement of clusters is guaranteed to converge. We provide bounds on the number of distance computations involved in the k-means algorithm. Further, each QPFS run is now cubic in number of clusters, which can be much smaller than actual number of features. Experiments on eight publicly available datasets show that our approach gives significant computational gains (both in time and memory), over standard QPFS as well as other state of the art feature selection methods, even while improving the overall accuracy.