Max-Margin Feature Selection

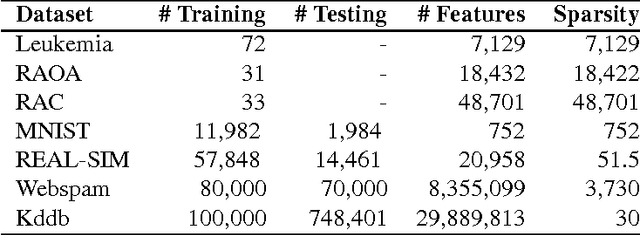
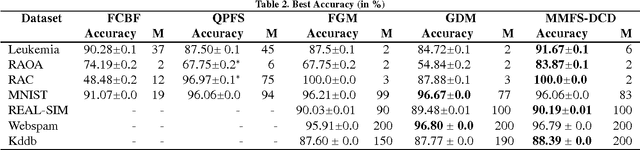
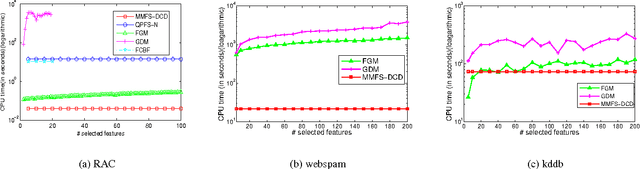
Many machine learning applications such as in vision, biology and social networking deal with data in high dimensions. Feature selection is typically employed to select a subset of features which im- proves generalization accuracy as well as reduces the computational cost of learning the model. One of the criteria used for feature selection is to jointly minimize the redundancy and maximize the rele- vance of the selected features. In this paper, we formulate the task of feature selection as a one class SVM problem in a space where features correspond to the data points and instances correspond to the dimensions. The goal is to look for a representative subset of the features (support vectors) which describes the boundary for the region where the set of the features (data points) exists. This leads to a joint optimization of relevance and redundancy in a principled max-margin framework. Additionally, our formulation enables us to leverage existing techniques for optimizing the SVM objective resulting in highly computationally efficient solutions for the task of feature selection. Specifically, we employ the dual coordinate descent algorithm (Hsieh et al., 2008), originally proposed for SVMs, for our formulation. We use a sparse representation to deal with data in very high dimensions. Experiments on seven publicly available benchmark datasets from a variety of domains show that our approach results in orders of magnitude faster solutions even while retaining the same level of accuracy compared to the state of the art feature selection techniques.