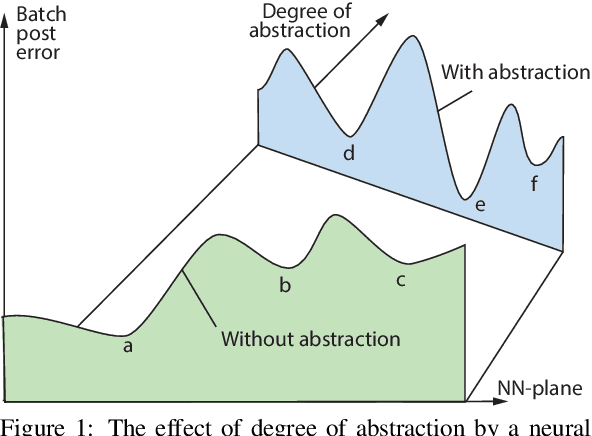
On "Deep Learning" Misconduct

This is a theoretical paper, as a companion paper of the plenary talk for the same conference ISAIC 2022. The problem addressed is the widespread so-called "Deep Learning" method -- training neural networks using error-backprop. The objective is to scientifically reason that the so-called "Deep Learning" contains fatal misconduct. In contrast to the main topic of the plenary talk, conscious learning (Weng, 2022b; Weng, 2022c) which develops a single network for a life (many tasks), "Deep Learning" trains multiple networks for each task. Although they may use different learning modes, including supervised, reinforcement and adversarial modes, almost all "Deep Learning" projects apparently suffer from the same misconduct, called "data deletion" and "test on training data". This paper reasons that "Deep Learning" was not tested by a disjoint test data set at all. Why? The so-called "test data set" was used in the Post-Selection step of the training stage! This paper establishes a theorem that a simple method called Pure-Guess Nearest Neighbor (PGNN) reaches any required errors on validation data set and test data set, including zero-error requirements, through the same "Deep Learning" misconduct, as long as the test data set is in the possession of the author and both the amount of storage space and the time of training are finite but unbounded. The misconduct of "Deep Learning" methods, clarified by the PGNN method, violates well-known protocols called transparency and cross-validation. The misconduct is fatal, because in the absence of any disjoint test, "Deep Learning" is clearly not generalizable.

Why Deep Learning's Performance Data Are Misleading

This is a theoretical paper, as a companion paper of the keynote talk at the same conference. In contrast to conscious learning, many projects in AI have employed deep learning many of which seem to give impressive performance data. This paper explains that such performance data are probably misleadingly inflated due to two possible misconducts: data deletion and test on training set. This paper clarifies what is data deletion in deep learning and what is test on training set in deep learning and why they are misconducts. A simple classification method is defined, called nearest neighbor with threshold (NNWT). A theorem is established that the NNWT method reaches a zero error on any validation set and any test set using Post-Selections, as long as the test set is in the possession of the author and both the amount of storage space and the time of training are finite but unbounded like with many deep learning methods. However, like many deep learning methods, the NNWT method has little generalization power. The evidence that misconducts actually took place in many deep learning projects is beyond the scope of this paper. Without a transparent account about freedom from Post-Selections, deep learning data are misleading.

Developmental Network Two, Its Optimality, and Emergent Turing Machines

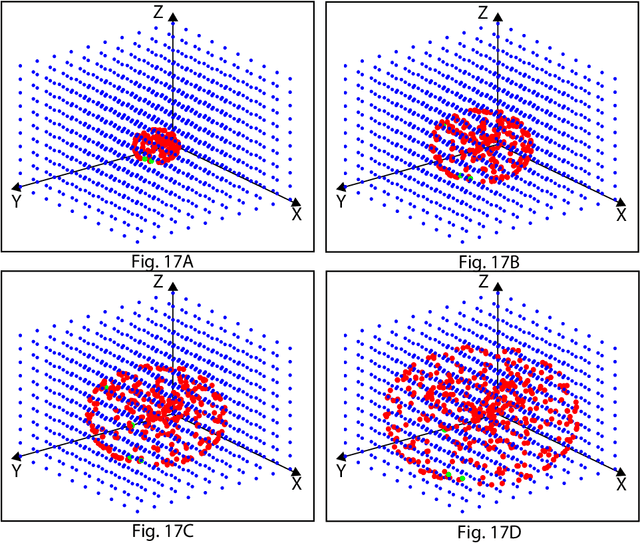
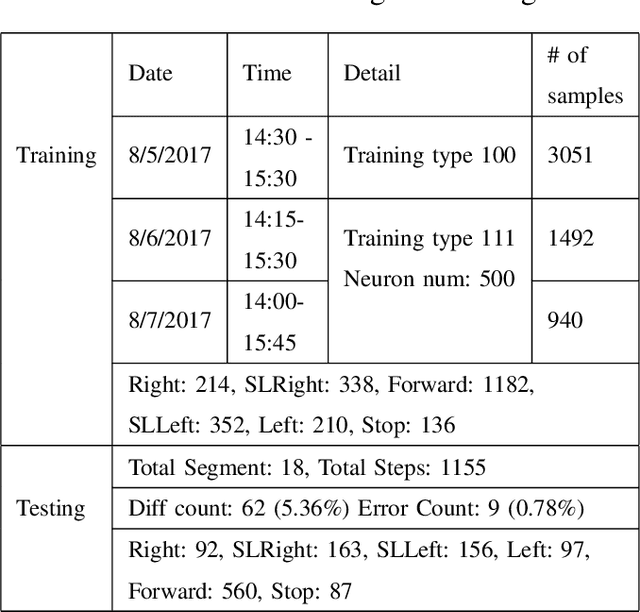
Strong AI requires the learning engine to be task non-specific and to automatically construct a dynamic hierarchy of internal features. By hierarchy, we mean, e.g., short road edges and short bush edges amount to intermediate features of landmarks; but intermediate features from tree shadows are distractors that must be disregarded by the high-level landmark concept. By dynamic, we mean the automatic selection of features while disregarding distractors is not static, but instead based on dynamic statistics (e.g. because of the instability of shadows in the context of landmark). By internal features, we mean that they are not only sensory, but also motor, so that context from motor (state) integrates with sensory inputs to become a context-based logic machine. We present why strong AI is necessary for any practical AI systems that work reliably in the real world. We then present a new generation of Developmental Networks 2 (DN-2). With many new novelties beyond DN-1, the most important novelty of DN-2 is that the inhibition area of each internal neuron is neuron-specific and dynamic. This enables DN-2 to automatically construct an internal hierarchy that is fluid, whose number of areas is not static as in DN-1. To optimally use the limited resource available, we establish that DN-2 is optimal in terms of maximum likelihood, under the condition of limited learning experience and limited resources. We also present how DN-2 can learn an emergent Universal Turing Machine (UTM). Together with the optimality, we present the optimal UTM. Experiments for real-world vision-based navigation, maze planning, and audition used DN-2. They successfully showed that DN-2 is for general purposes using natural and synthetic inputs. Their automatically constructed internal representation focuses on important features while being invariant to distractors and other irrelevant context-concepts.

Post Selections Using Test Sets and How Developmental Networks Avoid Them

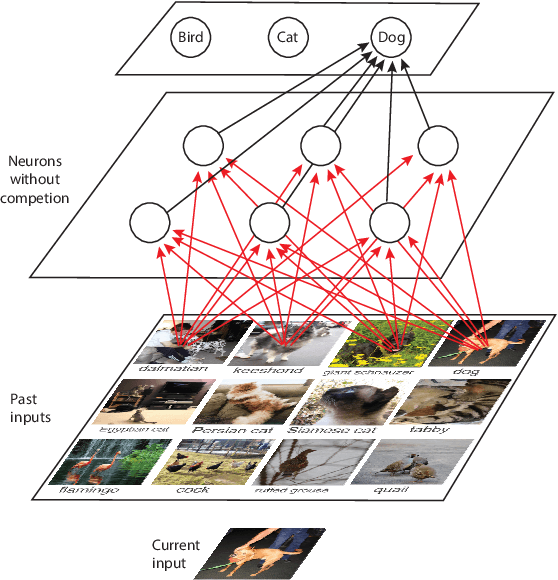
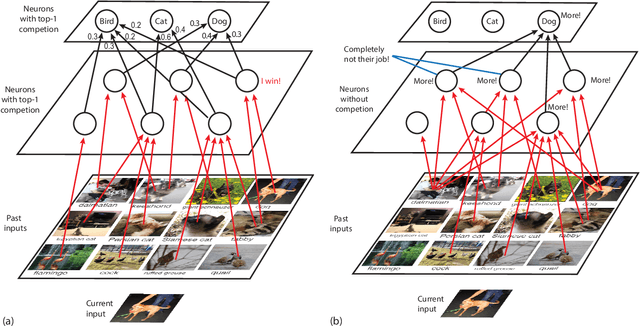
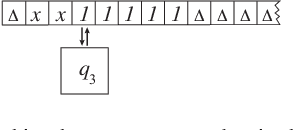
This paper raises a rarely reported practice in Artificial Intelligence (AI) called Post Selection Using Test Sets (PSUTS). Consequently, the popular error-backprop methodology in deep learning lacks an acceptable generalization power. All AI methods fall into two broad schools, connectionist and symbolic. The PSUTS fall into two kinds, machine PSUTS and human PSUTS. The connectionist school received criticisms for its "scruffiness" due to a huge number of network parameters and now the worse machine PSUTS; but the seemingly "clean" symbolic school seems more brittle because of a weaker generalization power using human PSUTS. This paper formally defines what PSUTS is, analyzes why error-backprop methods with random initial weights suffer from severe local minima, why PSUTS violates well-established research ethics, and how every paper that used PSUTS should have at least transparently reported PSUTS. For improved transparency in future publications, this paper proposes a new standard for performance evaluation of AI, called developmental errors for all networks trained, along with Three Learning Conditions: (1) an incremental learning architecture, (2) a training experience and (3) a limited amount of computational resources. Developmental Networks avoid PSUTS and are not "scruffy" because they drive Emergent Turing Machines and are optimal in the sense of maximum-likelihood across lifetime.

Conscious Intelligence Requires Lifelong Autonomous Programming For General Purposes

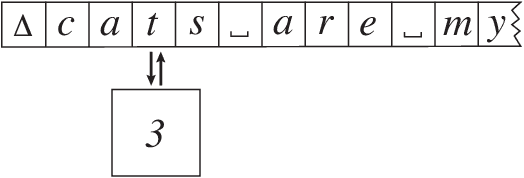
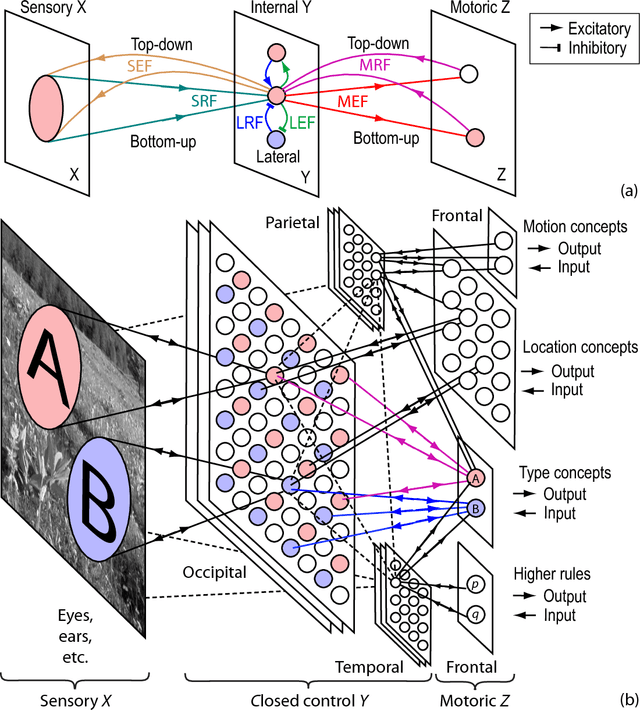
Universal Turing Machines [29, 10, 18] are well known in computer science but they are about manual programming for general purposes. Although human children perform conscious learning (i.e., learning while being conscious) from infancy [24, 23, 14, 4], it is unknown that Universal Turing Machiness can facilitate not only our understanding of Autonomous Programming For General Purposes (APFGP) by machines, but also enable early-age conscious learning. This work reports a new kind of AI---conscious learning AI from a machine's "baby" time. Instead of arguing what static tasks a conscious machine should be able to do during its "adulthood", this work suggests that APFGP is a computationally clearer and necessary criterion for us to judge whether a machine is capable of conscious learning so that it can autonomously acquire skills along its "career path". The results here report new concepts and experimental studies for early vision, audition, natural language understanding, and emotion, with conscious learning capabilities that are absent from traditional AI systems.

A Model for Auto-Programming for General Purposes

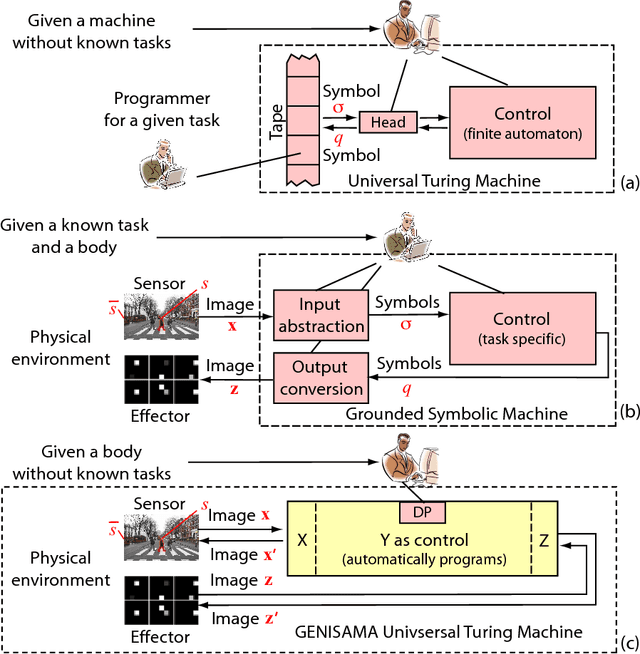
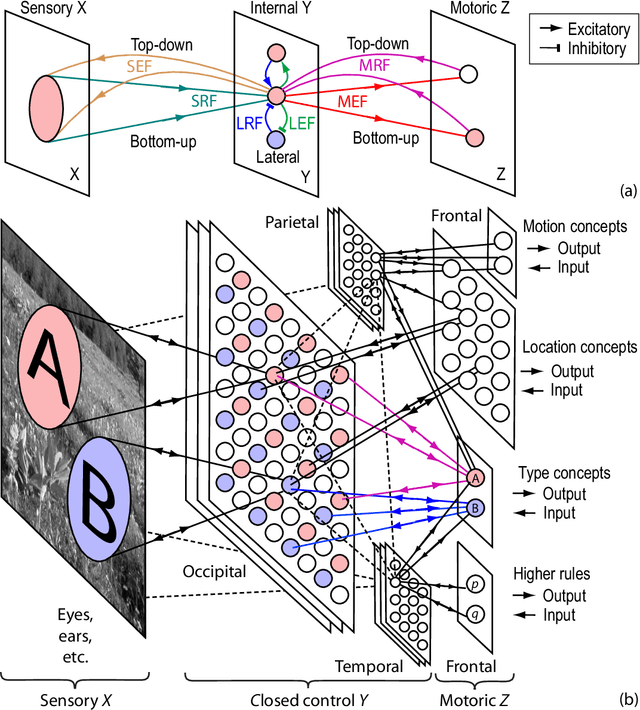
The Universal Turing Machine (TM) is a model for VonNeumann computers --- general-purpose computers. A human brain can inside-skull-automatically learn a universal TM so that he acts as a general-purpose computer and writes a computer program for any practical purposes. It is unknown whether a machine can accomplish the same. This theoretical work shows how the Developmental Network (DN) can accomplish this. Unlike a traditional TM, the TM learned by DN is a super TM --- Grounded, Emergent, Natural, Incremental, Skulled, Attentive, Motivated, and Abstractive (GENISAMA). A DN is free of any central controller (e.g., Master Map, convolution, or error back-propagation). Its learning from a teacher TM is one transition observation at a time, immediate, and error-free until all its neurons have been initialized by early observed teacher transitions. From that point on, the DN is no longer error-free but is always optimal at every time instance in the sense of maximal likelihood, conditioned on its limited computational resources and the learning experience. This letter also extends the Church-Turing thesis to automatic programming for general purposes and sketchily proved it.