A Model for Auto-Programming for General Purposes
Paper and Code
Oct 12, 2018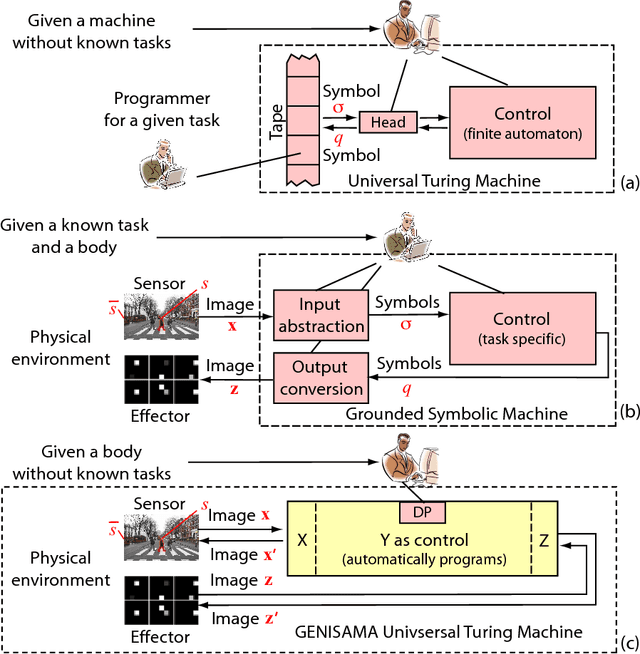
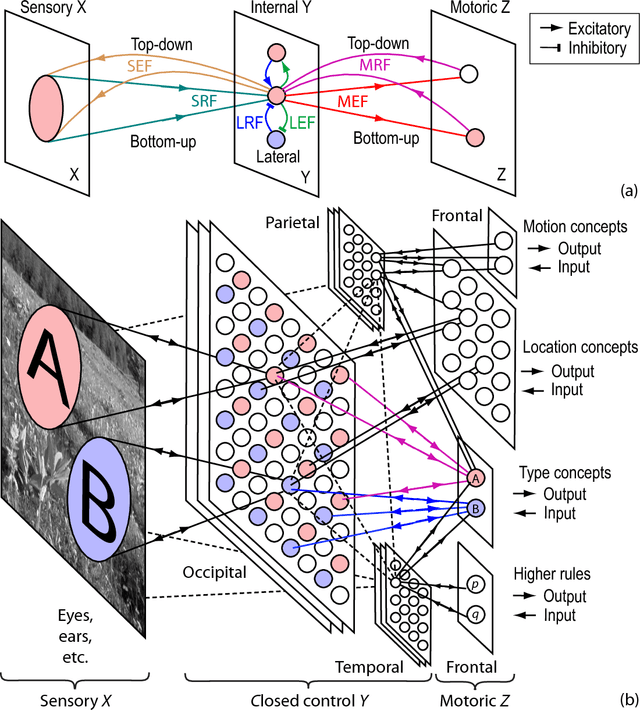


The Universal Turing Machine (TM) is a model for VonNeumann computers --- general-purpose computers. A human brain can inside-skull-automatically learn a universal TM so that he acts as a general-purpose computer and writes a computer program for any practical purposes. It is unknown whether a machine can accomplish the same. This theoretical work shows how the Developmental Network (DN) can accomplish this. Unlike a traditional TM, the TM learned by DN is a super TM --- Grounded, Emergent, Natural, Incremental, Skulled, Attentive, Motivated, and Abstractive (GENISAMA). A DN is free of any central controller (e.g., Master Map, convolution, or error back-propagation). Its learning from a teacher TM is one transition observation at a time, immediate, and error-free until all its neurons have been initialized by early observed teacher transitions. From that point on, the DN is no longer error-free but is always optimal at every time instance in the sense of maximal likelihood, conditioned on its limited computational resources and the learning experience. This letter also extends the Church-Turing thesis to automatic programming for general purposes and sketchily proved it.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge