Collision-Free Inverse Kinematics Through QP Optimization (iKinQP)

Robotic manipulators are often designed with more actuated degrees-of-freedom than required to fully control an end effector's position and orientation. These "redundant" manipulators can allow infinite joint configurations that satisfy a particular task-space position and orientation, providing more possibilities for the manipulator to traverse a smooth collision-free trajectory. However, finding such a trajectory is non-trivial because the inverse kinematics for redundant manipulators cannot typically be solved analytically. Many strategies have been developed to tackle this problem, including Jacobian pseudo-inverse method, rapidly-expanding-random tree (RRT) motion planning, and quadratic programming (QP) based methods. Here, we present a flexible inverse kinematics-based QP strategy (iKinQP). Because it is independent of robot dynamics, the algorithm is relatively light-weight, and able to run in real-time in step with torque control. Collisions are defined as kinematic trees of elementary geometries, making the algorithm agnostic to the method used to determine what collisions are in the environment. Collisions are treated as hard constraints which guarantees the generation of collision-free trajectories. Trajectory smoothness is accomplished through the QP optimization. Our algorithm was evaluated for computational efficiency, smoothness, and its ability to provide trackable trajectories. It was shown that iKinQP is capable of providing smooth, collision-free trajectories at real-time rates.

SpikePropamine: Differentiable Plasticity in Spiking Neural Networks

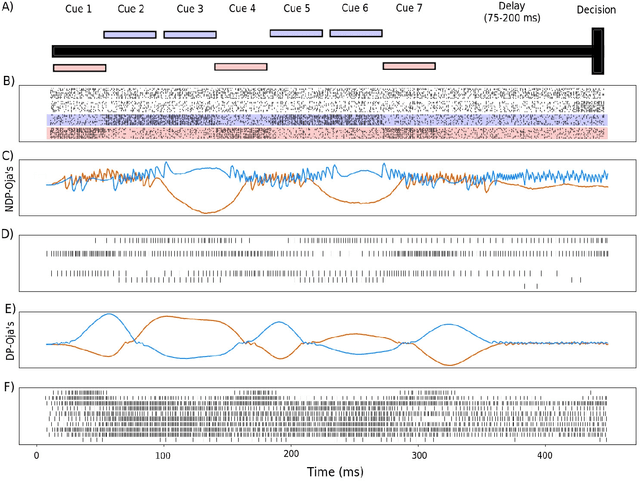
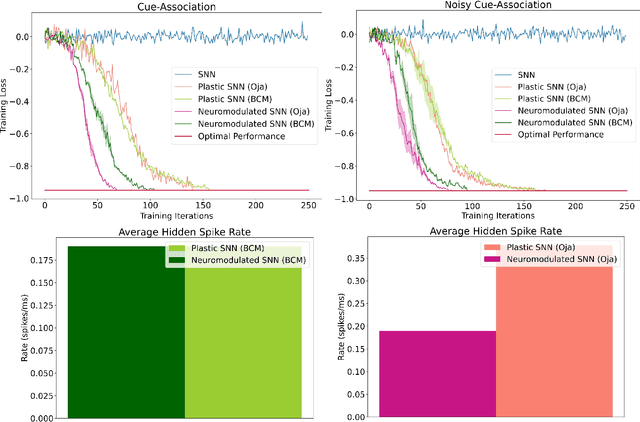
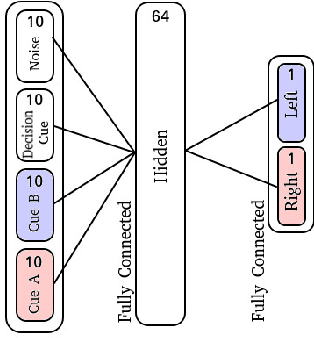
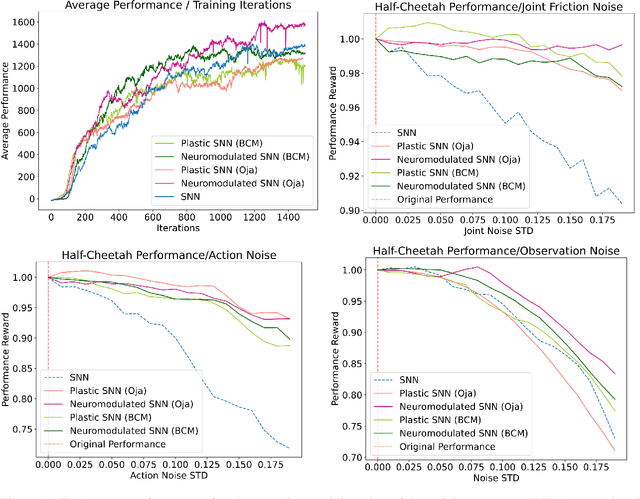
The adaptive changes in synaptic efficacy that occur between spiking neurons have been demonstrated to play a critical role in learning for biological neural networks. Despite this source of inspiration, many learning focused applications using Spiking Neural Networks (SNNs) retain static synaptic connections, preventing additional learning after the initial training period. Here, we introduce a framework for simultaneously learning the underlying fixed-weights and the rules governing the dynamics of synaptic plasticity and neuromodulated synaptic plasticity in SNNs through gradient descent. We further demonstrate the capabilities of this framework on a series of challenging benchmarks, learning the parameters of several plasticity rules including BCM, Oja's, and their respective set of neuromodulatory variants. The experimental results display that SNNs augmented with differentiable plasticity are sufficient for solving a set of challenging temporal learning tasks that a traditional SNN fails to solve, even in the presence of significant noise. These networks are also shown to be capable of producing locomotion on a high-dimensional robotic learning task, where near-minimal degradation in performance is observed in the presence of novel conditions not seen during the initial training period.