A Tractable Statistical Representation of IFTR Fading with Applications

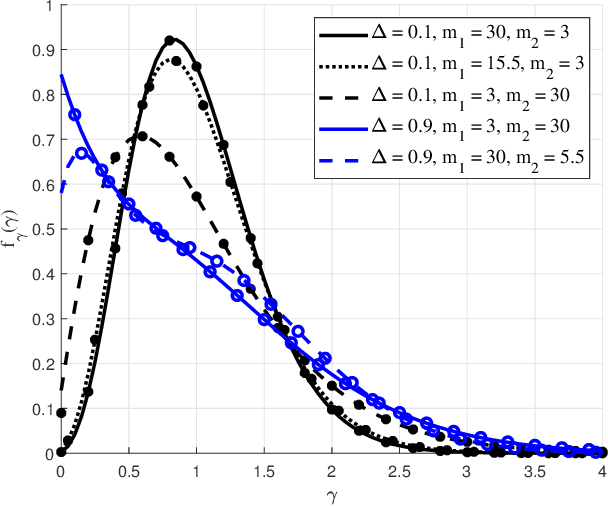
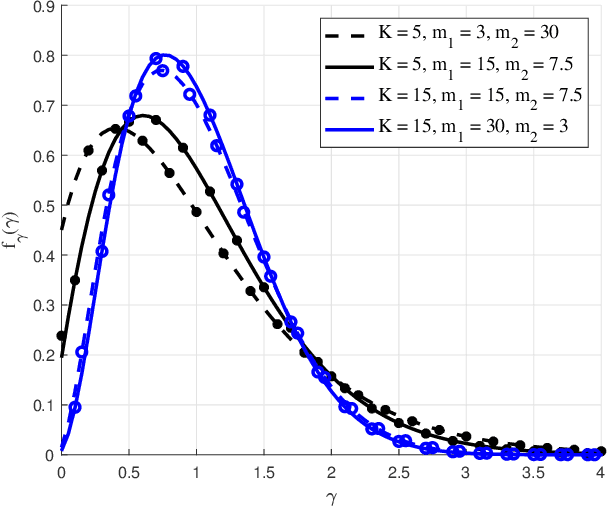
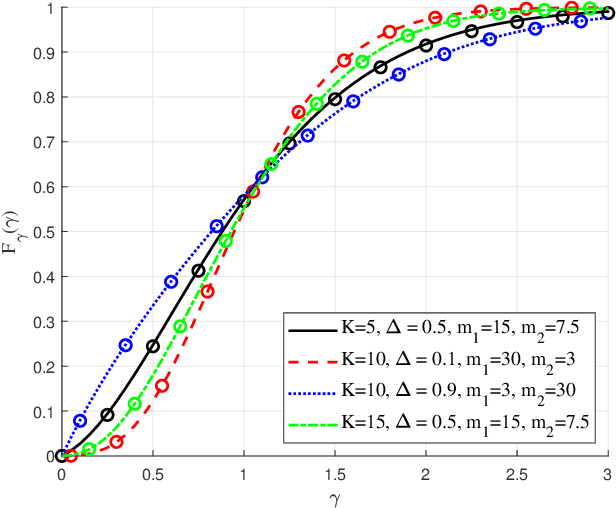
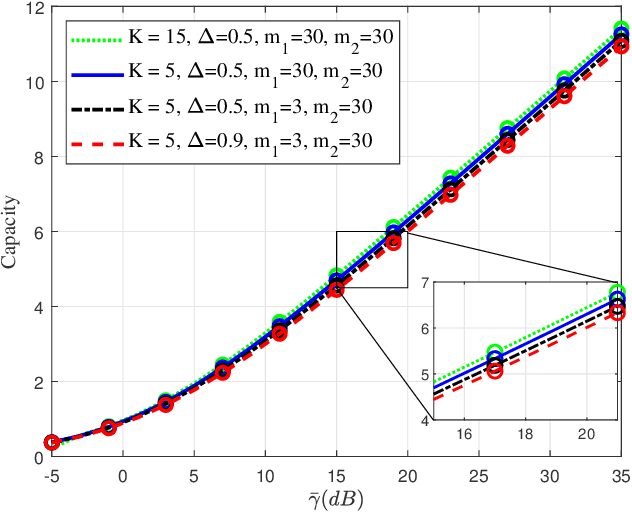
The recently introduced independent fluctuating two-ray (IFTR) fading model, consisting of two specular components fluctuating independently plus a diffuse component, has proven to provide an excellent fit to different wireless environments, including the millimeter-wave band. However, the original formulations of the probability density function (PDF) and cumulative distribution function (CDF) of this model are not applicable to all possible values of its defining parameters, and are given in terms of multifold generalized hypergeometric functions, which prevents their widespread use for the derivation of performance metric expressions. In this paper we present a new formulation of the IFTR model as a countable mixture of Gamma distributions which greatly facilitates the performance evaluation for this model in terms of the metrics already known for the much simpler and widely used Nakagami-m fading. Additionally, a closed-form expression is presented for the generalized moment generating function (GMGF), which permits to readily obtain all the moments of the distribution of the model, as well as several relevant performance metrics. Based on these new derivations, the IFTR model is evaluated for the average channel capacity, the outage probability with and without co-channel interference, and the bit error rate (BER), which are verified by Monte Carlo simulations.

The Multi-cluster Two-Wave Fading Model

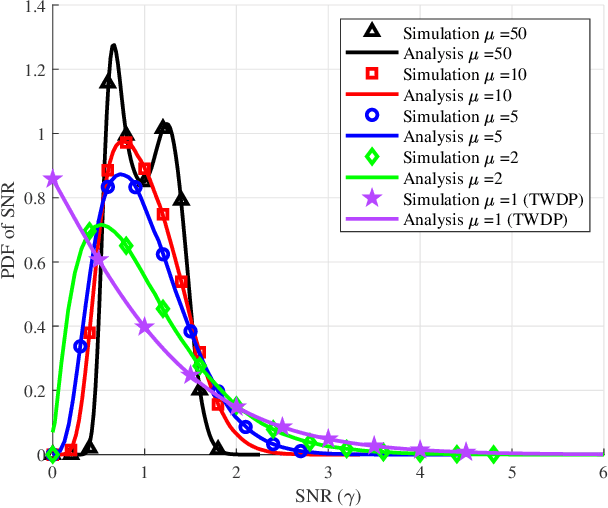
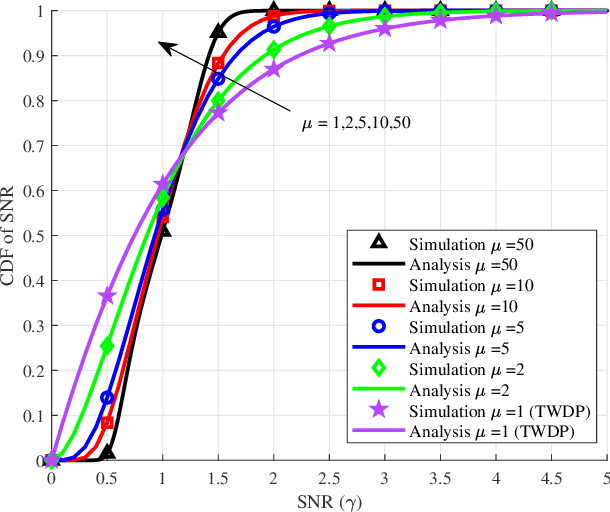
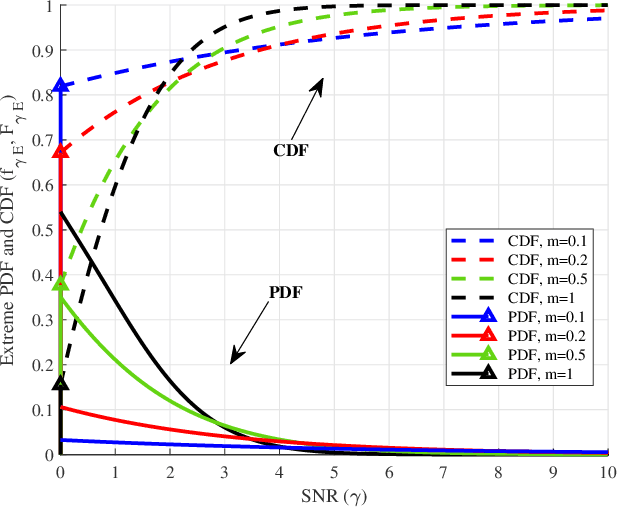
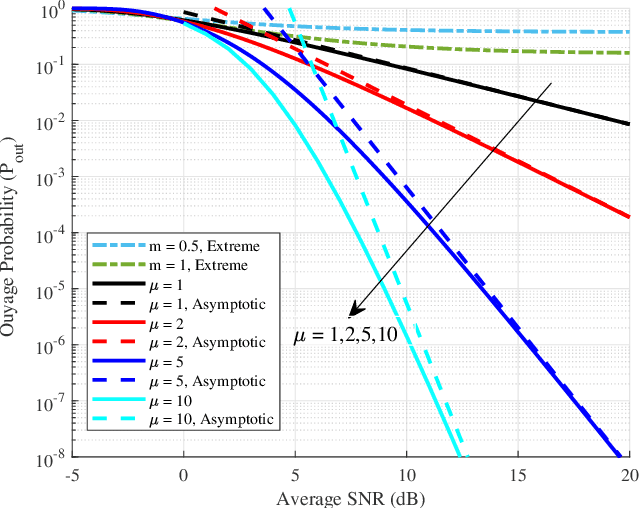
We introduce and characterize a natural generalization of the Two-Wave with Diffuse Power (TWDP) fading model, by allowing that the incident waves arrive in different clusters. The newly proposed model, referred to as the Multi-cluster Two-Wave (MTW) fading model, generalizes both the TWDP and the kappa-mu models under a common umbrella. The special case on which the model parameters reach extreme values is also analyzed, aimed to model harsh fading conditions reported in experimental measurements obtained in enclosed environments. The chief probability functions of both the MTW and the MTW Extreme fading models are obtained, including the probability density function, the cumulative distribution function and the generalized moment-generating function. A number of applications for these models are exemplified, including outage probability in interference-limited scenarios, energy detection, and composite fading modeling.

The Fluctuating Two-Ray Fading Model with Independent Specular Components

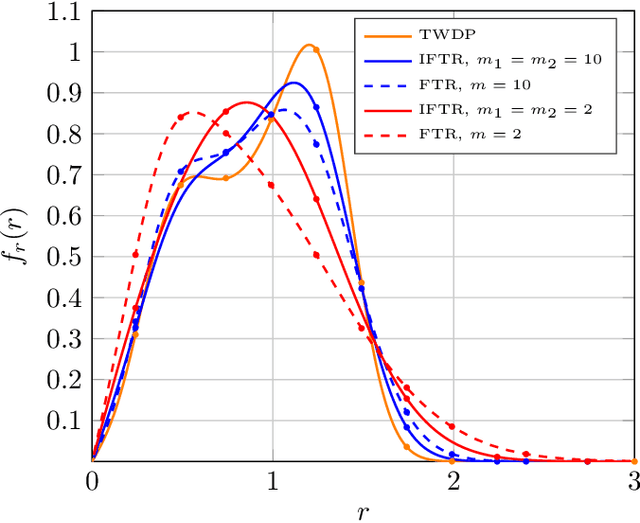
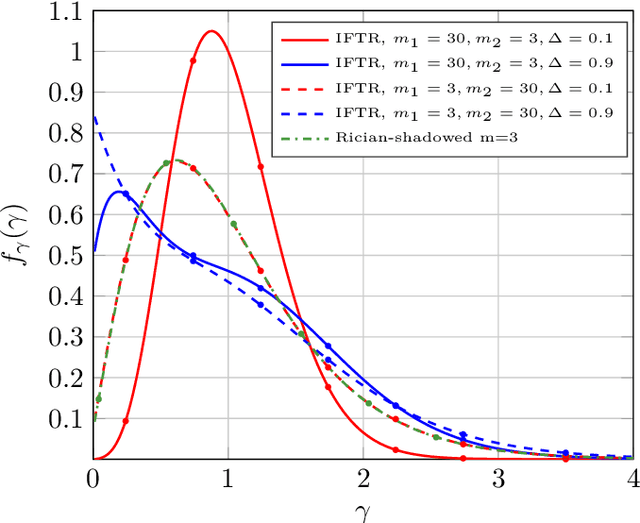
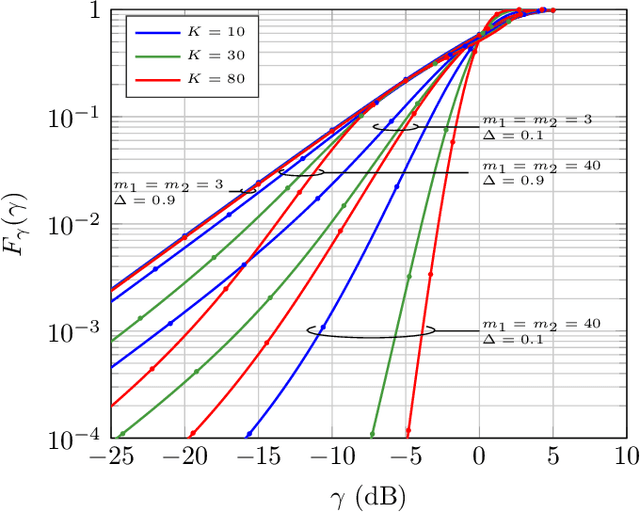
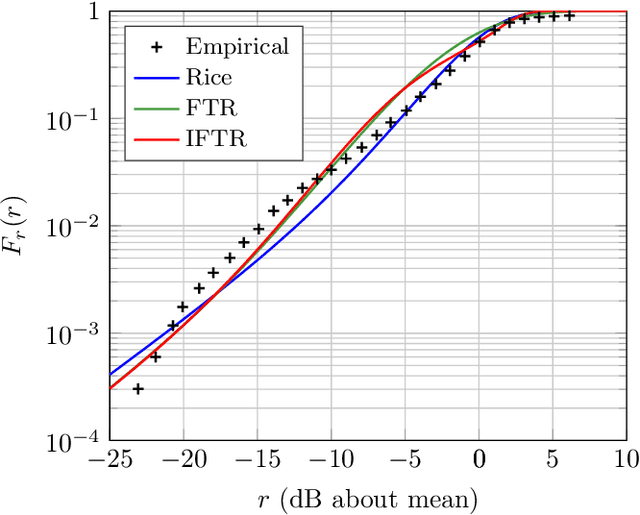
We introduce and characterize the independent fluctuating two-ray (IFTR) fading model, a class of fading models consisting of two specular components which fluctuate independently, plus a diffuse component modeled as a complex Gaussian random variable. The IFTR model complements the popular fluctuating two-ray (FTR) model, on which the specular components are fully correlated and fluctuate jointly. The chief probability functions of the received SNR in IFTR fading, including the PDF, CDF and MGF, are expressed in closed-form, having a functional form similar to other state-of-the-art fading models. Then, the IFTR model is empirically validated using multiple channels measured in rather diverse scenarios, including line of sight (LOS) millimeter-wave, land mobile satellite (LMS) and underwater acoustic communication (UAC), showing a better fit than the original FTR model and other models previously used in these environments. Additionally, the performance of wireless communication systems operating under IFTR fading is evaluated in closed-form in two scenarios: (i) exact and asymptotic bit error rate for a family of coherent modulations; and (ii) exact and asymptotic outage probability.

Composite IG/FTR Channel Performance in Wireless Communication Systems

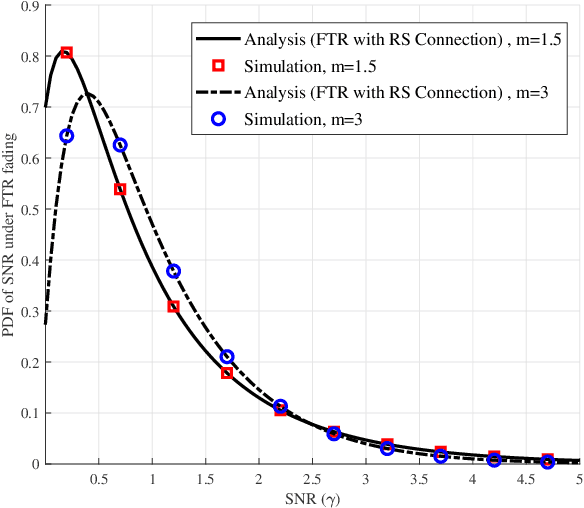
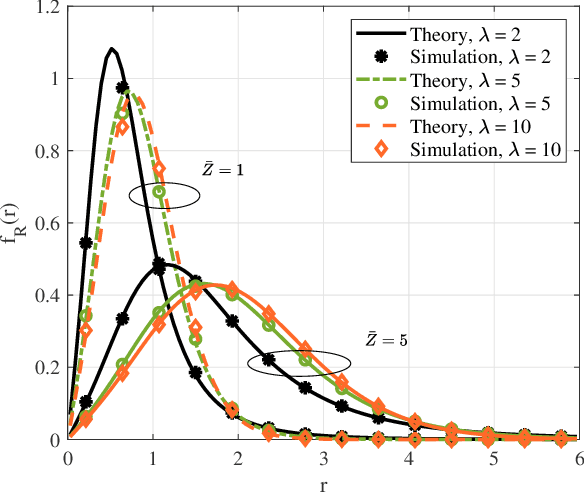
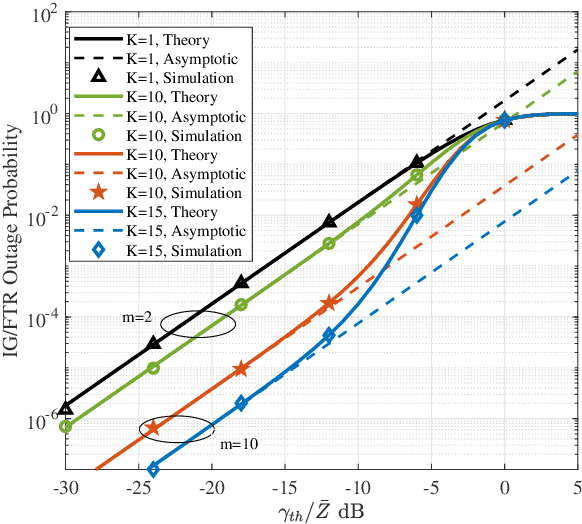
We present a composite wireless fading model encompassing multipath fading and shadowing based on fluctuating two-ray (FTR) fading and inverse gamma (IG) shadowing. We first determine an alternative framework for the statistical characterization and performance evaluation of the FTR fading model, which is based on the fact that the FTR fading distribution can be described as an underlying Rician Shadowed (RS) distribution with continuously varying parameter Kr (ratio of specular to diffuse components). We demonstrate that this new formulation permits to obtain a closed-form expression of the generalized moment generating function (GMGF) of the FTR model, from which the PDF and CDF of the composite IG/FTR model can be obtained in closed-form. The exact and asymptotic outage probability of the IG/FTR model are analyzed and verified by Monte Carlo simulations.

Alternative Formulations for the Fluctuating Two-Ray Fading Model

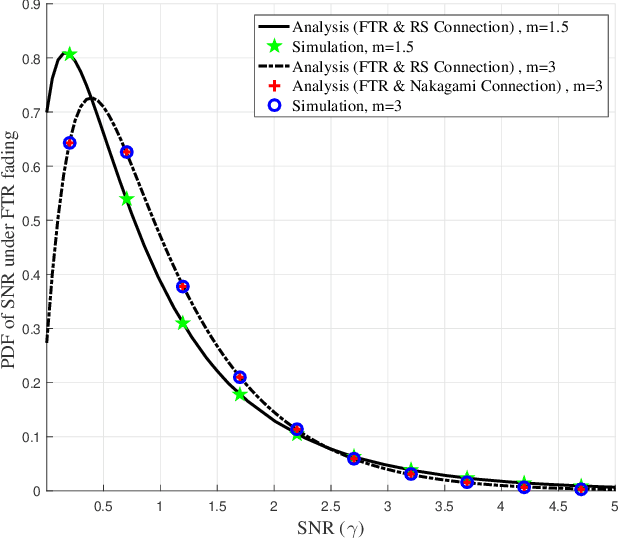
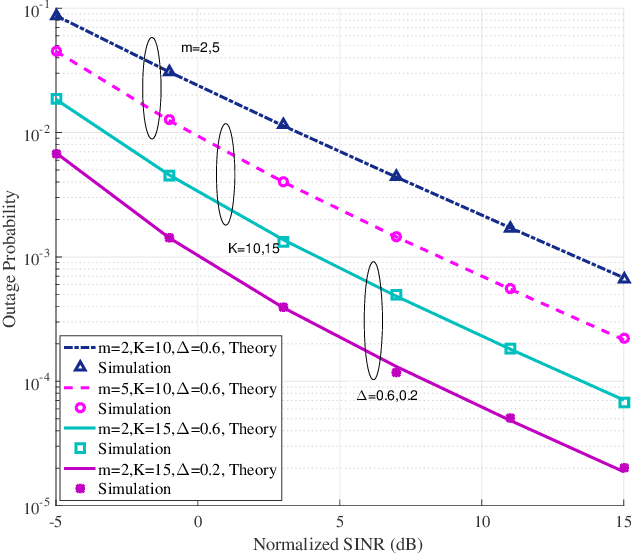
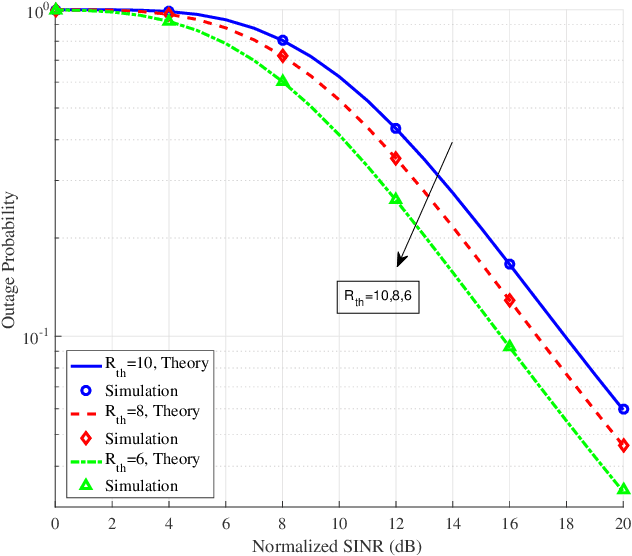
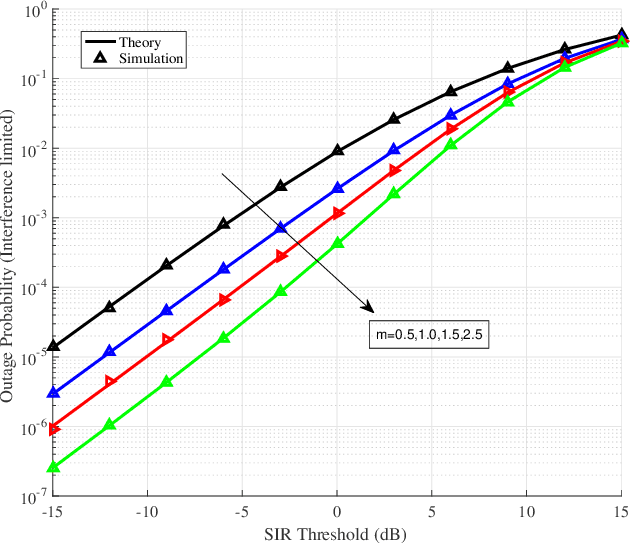
We present two alternative formulations for the distribution of the fluctuating two-ray (FTR) fading model, which simplify its statistical characterization and subsequent use for performance evaluation. New expressions for the probability density function (PDF) and cumulative distribution function of the FTR model are obtained based on the observation that the FTR fading distribution is described, for arbitrary $m$, as an underlying Rician Shadowed (RS) distribution with continuously varying parameter $K$, while for the special case of $m$ being an integer, the FTR fading model is described in terms of a finite number of underlying squared Nakagami-$m$ distributions. It is shown that the chief statistics and any performance metric that are computed by averaging over the PDF of the FTR fading model can be expressed in terms of a finite-range integral over the corresponding statistic or performance metric for the RS (for arbitrary $m$) or the Nakagami-$m$ (for integer $m$) fading models, which have a simpler analytical characterization than the FTR model and for which many results are available in closed-form. New expressions for some Laplace-domain statistics of interest are also obtained; these are used to exemplify the practical relevance of this new formulation for performance analysis.

A Fluctuating Line-of-Sight Fading Model with Double-Rayleigh Diffuse Scattering

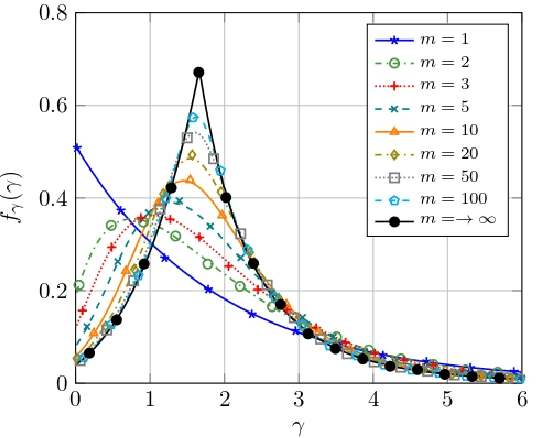
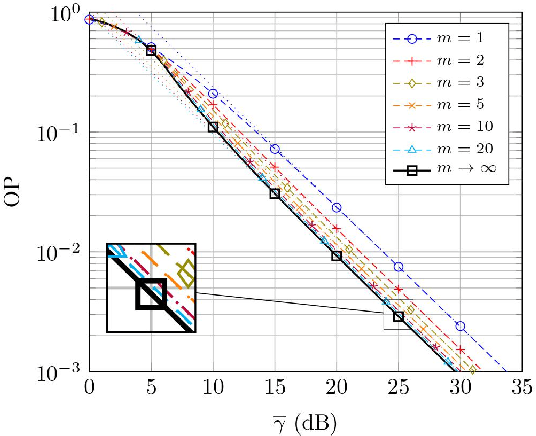
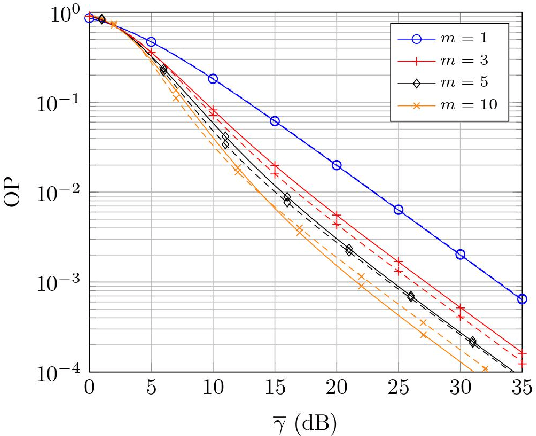
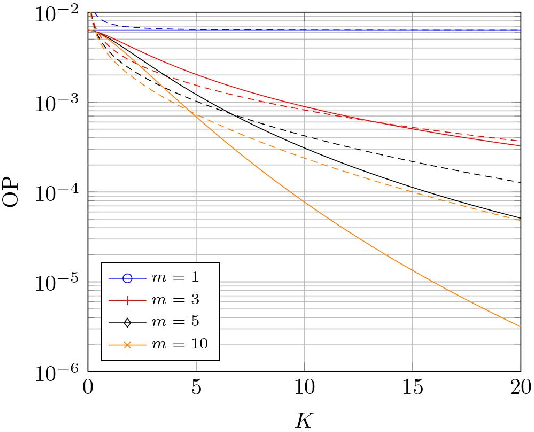
We introduce the fdRLoS fading model as a natural generalization of the double-Rayleigh with line-of-sight fading model, on which the constant-amplitude line-of-sight component is now allowed to randomly fluctuate. We discuss the key benefits of the fdRLoS fading model here formulated over the state of the art, and provide an analytical characterization of its chief probability functions. We analyze the effect of the fading parameters that define the model, and discuss their impact on the performance of wireless communication systems.