Tangential Velocity Estimation Using Near-Field Automotive Radar Model

This work investigates the problem of tangential velocity estimation in automotive radar systems, addressing the limitations of conventionally considered models. Conventional automotive radars are usually based on far-field models and estimate the target's range, radial velocity, and direction-of-arrival (DOA) but are not able to estimate the tangential component of the target 2-D velocity, which is a critical parameter for reliable perception of dynamic environments. To address this challenge, we introduce the near-field radar model, which considers various migration elements in range, radial velocity, and Doppler along time and space. Conventionally, these migration effects result in smearing of the likelihood function for estimating the target parameters. However, if the model is correctly specified, these migration effects are informative for tangential velocity estimation. We conduct an identifiability analysis for tangential velocity estimation using the Cram\'er-Rao bound and ambiguity function. The insights from this study motivate the use of a separated array configuration and the development of a computationally efficient maximum likelihood based algorithm designed to utilize target migrations for tangential velocity estimation, while maintaining practical computational complexity. In addition to tangential velocity estimation, the proposed algorithm mitigates likelihood smearing in range, radial velocity, and Doppler. Simulations validate the theoretical feasibility study, and evaluate the algorithms' performance in both single- and multi-target scenarios. The proposed approach improves the accuracy and reliability of automotive radars, enhancing situational awareness for advanced driver assistance systems and autonomous vehicles.

Model Selection via MCRB Optimization

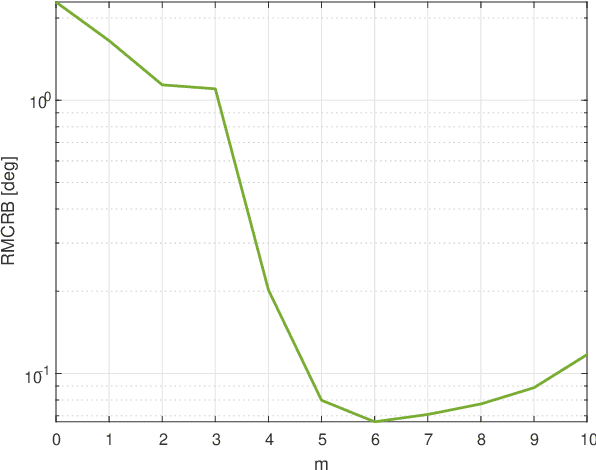
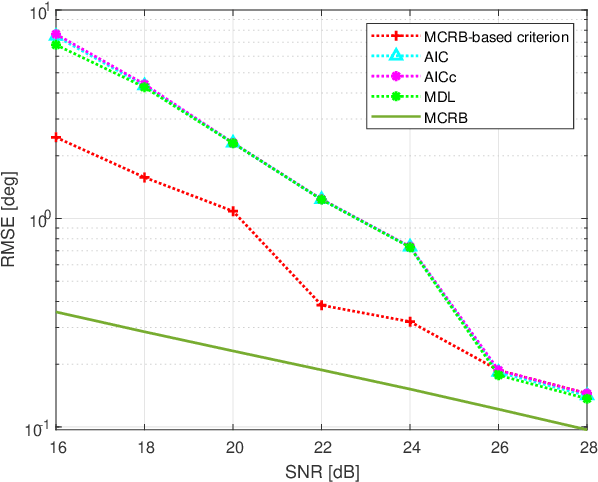
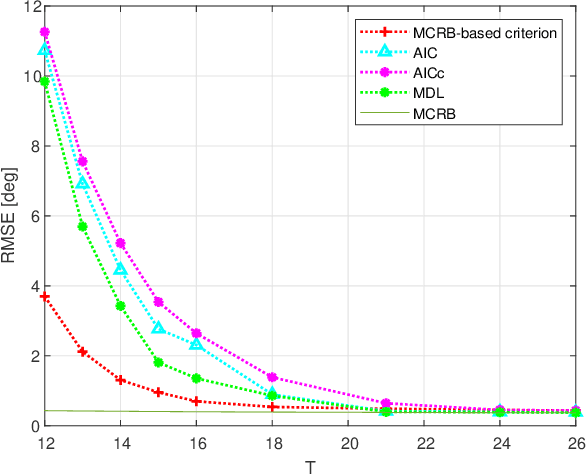
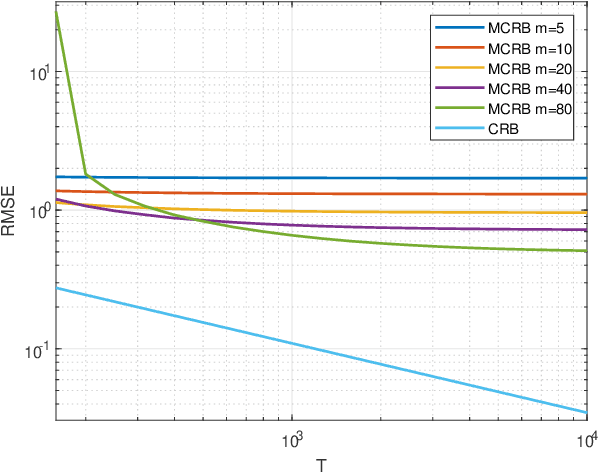
In many estimation theory and statistical analysis problems, the true data model is unknown, or partially unknown. To describe the model generating the data, parameterized models of some degree are used. A question that arises is which model should be used to best approximate the true model, a.k.a. model selection. In the field of machine learning, it is encountered in the form of architecture types of neural networks, number of model parameters, etc. In this paper, we propose a new model selection criterion, based on the misspecified Cramer-Rao bound (MCRB) for mean-squared-error (MSE) performance. The criterion selects the model in which the bound on the estimated parameters MSE is the lowest, compared to other candidate models. Its goal is to minimize the MSE with-respect-to (w.r.t.) the model. The criterion is applied to the problems of direction-of-arrival (DOA) estimation under unknown clutter / interference, and spectrum estimation of auto-regressive (AR) model. It is shown to incorporate the bias-variance trade-off, and outperform the Akaike information criterion (AIC), finite-sample corrected AIC (AICc), and minimum description length (MDL) in terms of MSE performance.

MCRB for Parameter Estimation from One-Bit Quantized and Oversampled Measurements

One-bit quantization has garnered significant attention in recent years for various signal processing and communication applications. Estimating model parameters from one bit quantized data can be challenging, particularly when the quantization process is explicitly accounted for in the estimator. In many cases, the estimator disregards quantization effects, leading to model misspecification. Consequently, estimation errors arise from both quantization and misspecification. Traditional performance bounds, such as the Cramer-Rao bound (CRB), fail to capture the impact of misspecification on estimation performance. To address this limitation, we derive the misspecified CRB (MCRB) for parameter estimation in a quantized data model consisting of a signal component in additive Gaussian noise. We apply this bound to direction-of-arrival estimation using quantized measurements from a sensor array and to frequency estimation with oversampled quantized data. The simulations show that the MCRB is asymptotically achieved by the mean-squared-error of the misspecified maximum-likelihood estimator. Our results demonstrate that, unlike in finely quantized scenarios, oversampling can significantly enhance the estimation performance in the presence of misspecified one-bit quantized measurements.

Asymptotically Tight Bayesian Cramér-Rao Bound

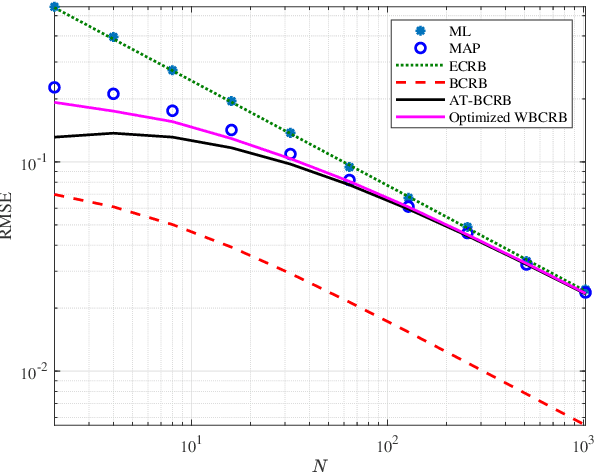
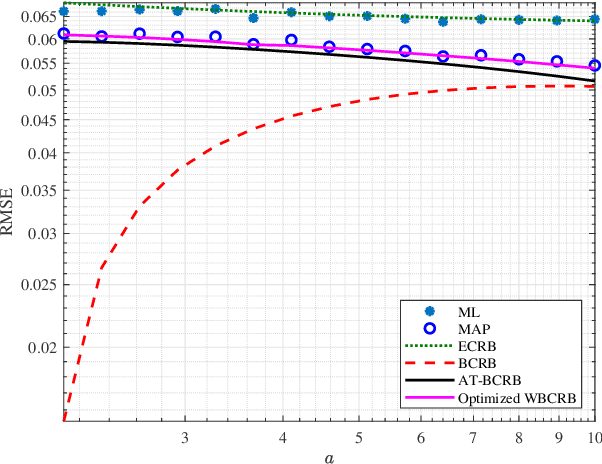
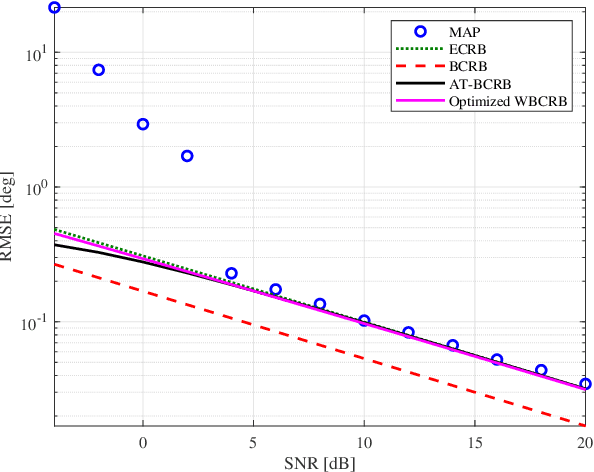
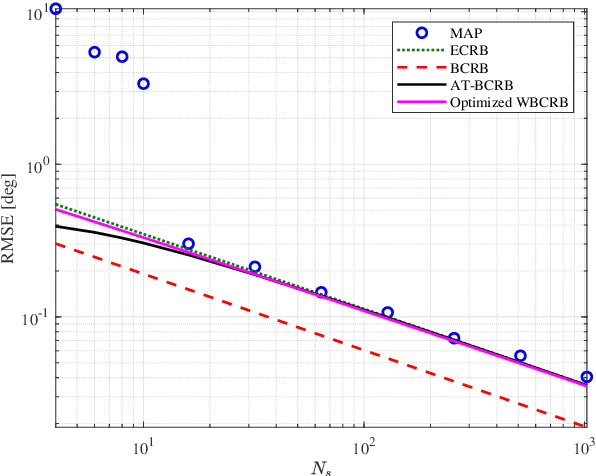
Performance bounds for parameter estimation play a crucial role in statistical signal processing theory and applications. Two widely recognized bounds are the Cram\'{e}r-Rao bound (CRB) in the non-Bayesian framework, and the Bayesian CRB (BCRB) in the Bayesian framework. However, unlike the CRB, the BCRB is asymptotically unattainable in general, and its equality condition is restrictive. This paper introduces an extension of the Bobrovsky--Mayer-Wolf--Zakai class of bounds, also known as the weighted BCRB (WBCRB). The WBCRB is optimized by tuning the weighting function in the scalar case. Based on this result, we propose an asymptotically tight version of the bound called AT-BCRB. We prove that the AT-BCRB is asymptotically attained by the maximum {\it a-posteriori} probability (MAP) estimator. Furthermore, we extend the WBCRB and the AT-BCRB to the case of vector parameters. The proposed bounds are evaluated in several fundamental signal processing examples, such as variance estimation of white Gaussian process, direction-of-arrival estimation, and mean estimation of Gaussian process with unknown variance and prior statistical information. It is shown that unlike the BCRB, the proposed bounds are asymptotically attainable and coincide with the expected CRB (ECRB). The ECRB, which imposes uniformly unbiasedness, cannot serve as a valid lower bound in the Bayesian framework, while the proposed bounds are valid for any estimator.

MCRB on DOA Estimation for Automotive MIMO Radar in the Presence of Multipath

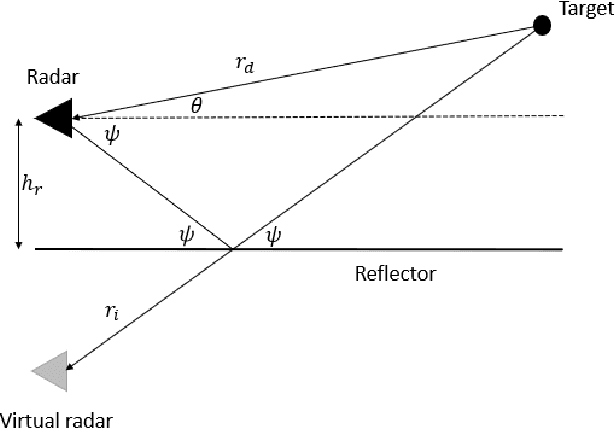
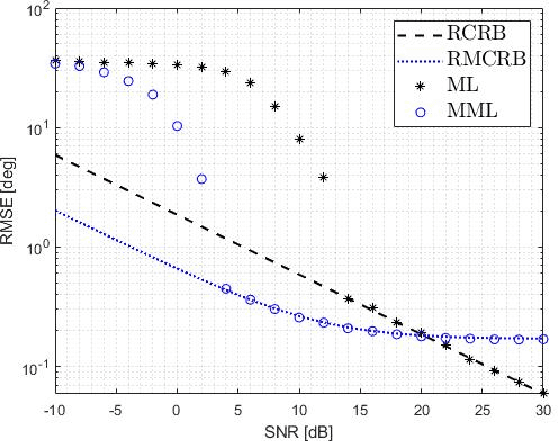
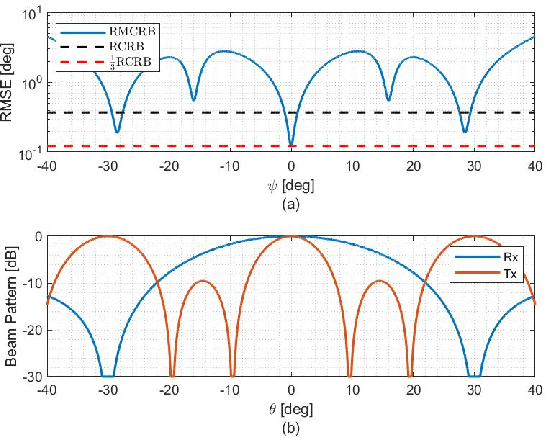
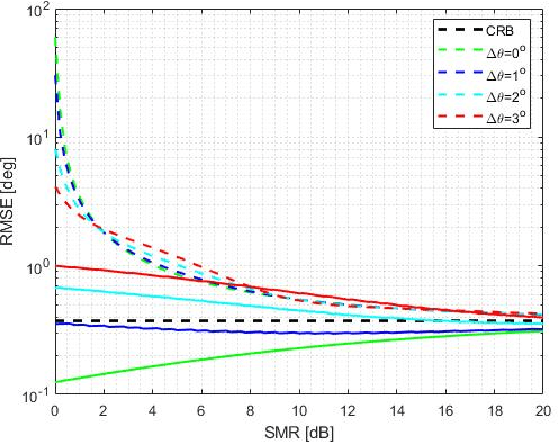
Autonomous driving and advanced active safety features require accurate high-resolution sensing capabilities. Automotive radars are the key component of the vehicle sensing suit. However, when these radars operate in proximity to flat surfaces, such as roads and guardrails, they experience a multipath phenomenon that can degrade the accuracy of the direction-of-arrival (DOA) estimation. Presence of multipath leads to misspecification in the radar data model, resulting in estimation performance degradation, which cannot be reliably predicted by conventional performance bounds. In this paper, the misspecified Cram\'er-Rao bound (MCRB), which accounts for model misspecification, is derived for the problem of DOA estimation in the presence of multipath which is ignored by the estimator. Analytical relations between the MCRB and the Cram\'er-Rao bound are established, and the DOA estimation performance degradation due to multipath is investigated. The results show that the MCRB reliably predicts the asymptotic performance of the misspecified maximum-likelihood estimator and therefore, can serve as an efficient tool for automotive radar performance evaluation and system design.

Barankin-Type Bound for Constrained Parameter Estimation

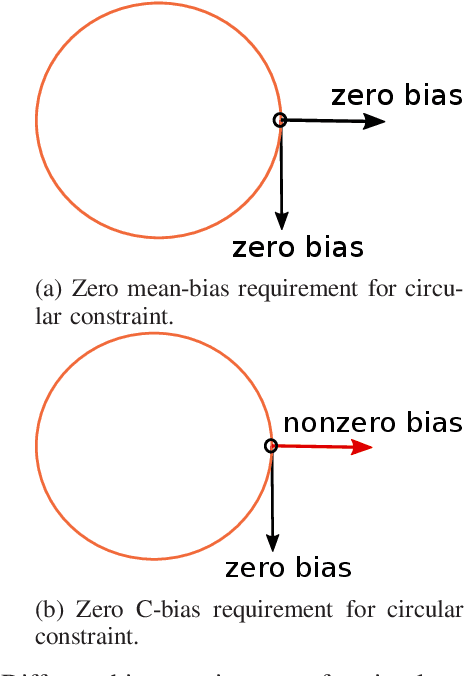
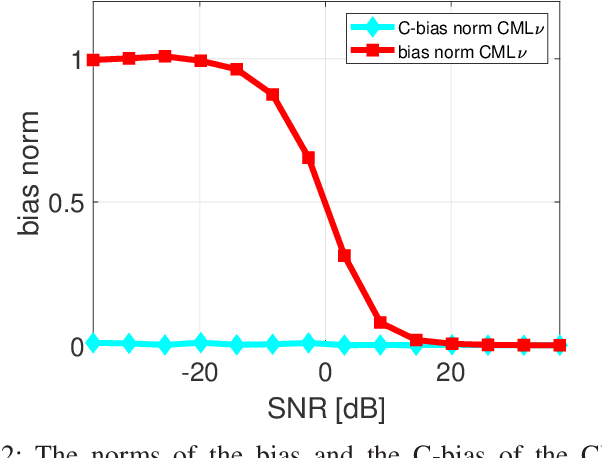
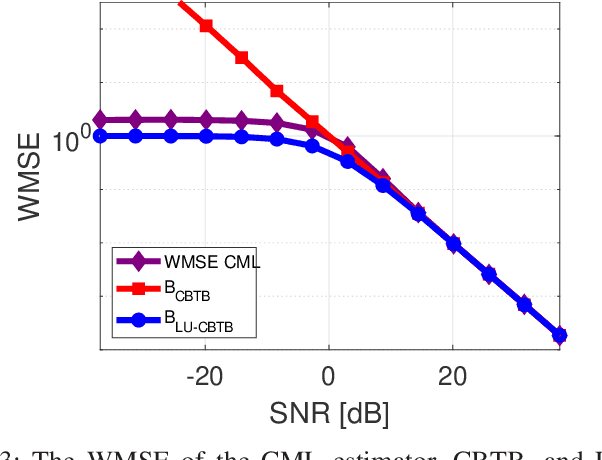
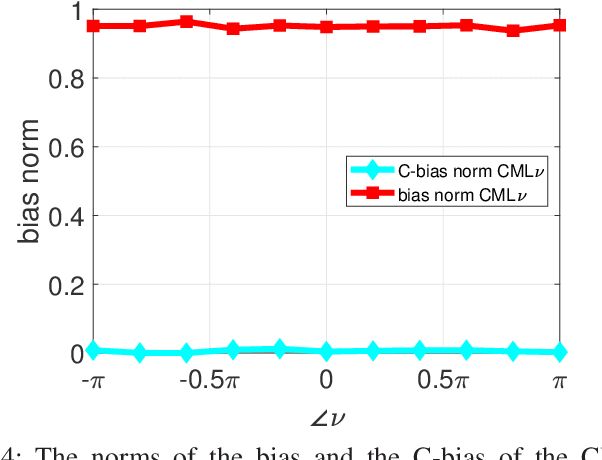
In constrained parameter estimation, the classical constrained Cramer-Rao bound (CCRB) and the recent Lehmann-unbiased CCRB (LU-CCRB) are lower bounds on the performance of mean-unbiased and Lehmann-unbiased estimators, respectively. Both the CCRB and the LU-CCRB require differentiability of the likelihood function, which can be a restrictive assumption. Additionally, these bounds are local bounds that are inappropriate for predicting the threshold phenomena of the constrained maximum likelihood (CML) estimator. The constrained Barankin-type bound (CBTB) is a nonlocal mean-squared-error (MSE) lower bound for constrained parameter estimation that does not require differentiability of the likelihood function. However, this bound requires a restrictive mean-unbiasedness condition in the constrained set. In this work, we propose the Lehmann-unbiased CBTB (LU-CBTB) on the weighted MSE. This bound does not require differentiability of the likelihood function and assumes Lehmann-unbiasedness, which is less restrictive than the CBTB mean-unbiasedness. We show that the LU-CBTB is tighter than or equal to the LU-CCRB and coincides with the CBTB for linear constraints. For nonlinear constraints the LU-CBTB and the CBTB are different and the LU-CBTB can be a lower bound on the WMSE of constrained estimators in cases, where the CBTB is not. In the simulations, we consider direction-of-arrival estimation of an unknown constant modulus discrete signal. In this case, the likelihood function is not differentiable and constrained Cramer-Rao-type bounds do not exist, while CBTBs exist. It is shown that the LU-CBTB better predicts the CML estimator performance than the CBTB, since the CML estimator is Lehmann-unbiased but not mean-unbiased.

Neural Network-Based DOA Estimation in the Presence of Non-Gaussian Interference

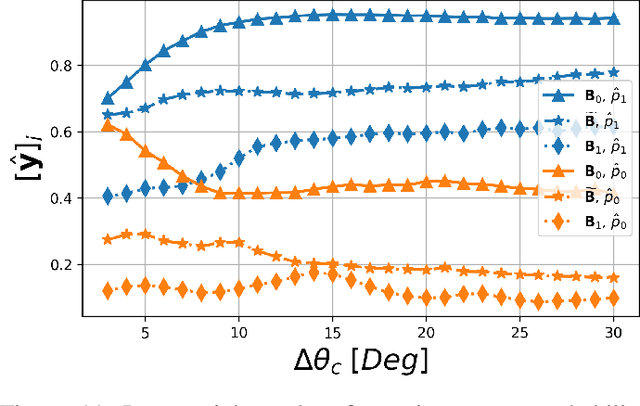
This work addresses the problem of direction-of-arrival (DOA) estimation in the presence of non-Gaussian, heavy-tailed, and spatially-colored interference. Conventionally, the interference is considered to be Gaussian-distributed and spatially white. However, in practice, this assumption is not guaranteed, which results in degraded DOA estimation performance. Maximum likelihood DOA estimation in the presence of non-Gaussian and spatially colored interference is computationally complex and not practical. Therefore, this work proposes a neural network (NN) based DOA estimation approach for spatial spectrum estimation in multi-source scenarios with a-priori unknown number of sources in the presence of non-Gaussian spatially-colored interference. The proposed approach utilizes a single NN instance for simultaneous source enumeration and DOA estimation. It is shown via simulations that the proposed approach significantly outperforms conventional and NN-based approaches in terms of probability of resolution, estimation accuracy, and source enumeration accuracy in conditions of low SIR, small sample support, and when the angular separation between the source DOAs and the spatially-colored interference is small.