Gaussian Copula Models for Nonignorable Missing Data Using Auxiliary Marginal Quantiles

We present an approach for modeling and imputation of nonignorable missing data under Gaussian copulas. The analyst posits a set of quantiles of the marginal distributions of the study variables, for example, reflecting information from external data sources or elicited expert opinion. When these quantiles are accurately specified, we prove it is possible to consistently estimate the copula correlation and perform multiple imputation in the presence of nonignorable missing data. We develop algorithms for estimation and imputation that are computationally efficient, which we evaluate in simulation studies of multiple imputation inferences. We apply the model to analyze associations between lead exposure levels and end-of-grade test scores for 170,000 students in North Carolina. These measurements are not missing at random, as children deemed at-risk for high lead exposure are more likely to be measured. We construct plausible marginal quantiles for lead exposure using national statistics provided by the Centers for Disease Control and Prevention. Complete cases and missing at random analyses appear to underestimate the relationships between certain variables and end-of-grade test scores, while multiple imputation inferences under our model support stronger adverse associations between lead exposure and educational outcomes.

Bayesian Quantile Regression with Subset Selection: A Posterior Summarization Perspective

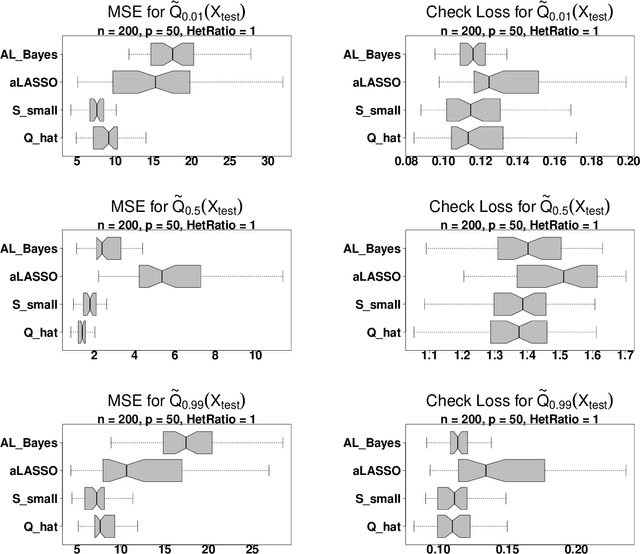
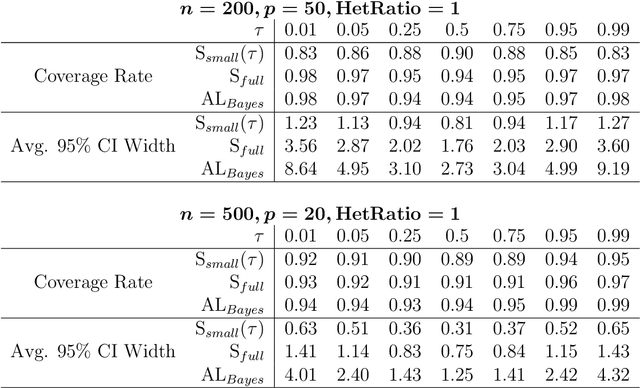
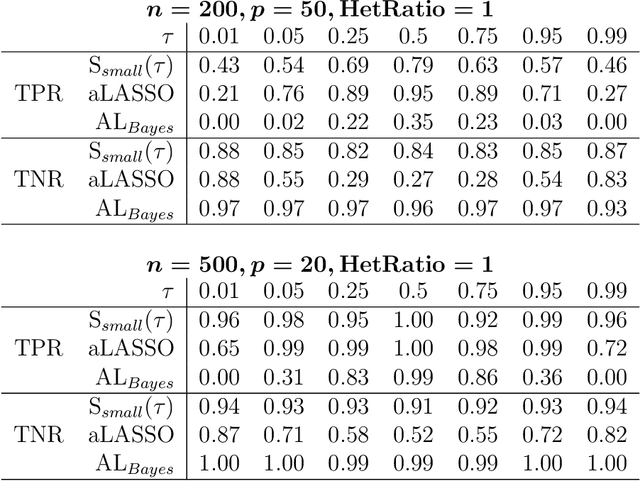
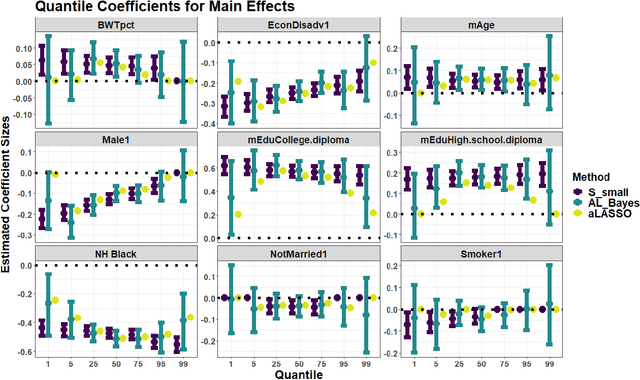
Quantile regression is a powerful tool for inferring how covariates affect specific percentiles of the response distribution. Existing methods either estimate conditional quantiles separately for each quantile of interest or estimate the entire conditional distribution using semi- or non-parametric models. The former often produce inadequate models for real data and do not share information across quantiles, while the latter are characterized by complex and constrained models that can be difficult to interpret and computationally inefficient. Further, neither approach is well-suited for quantile-specific subset selection. Instead, we pose the fundamental problems of linear quantile estimation, uncertainty quantification, and subset selection from a Bayesian decision analysis perspective. For any Bayesian regression model, we derive optimal and interpretable linear estimates and uncertainty quantification for each model-based conditional quantile. Our approach introduces a quantile-focused squared error loss, which enables efficient, closed-form computing and maintains a close relationship with Wasserstein-based density estimation. In an extensive simulation study, our methods demonstrate substantial gains in quantile estimation accuracy, variable selection, and inference over frequentist and Bayesian competitors. We apply these tools to identify the quantile-specific impacts of social and environmental stressors on educational outcomes for a large cohort of children in North Carolina.