Gaussian Copula Models for Nonignorable Missing Data Using Auxiliary Marginal Quantiles

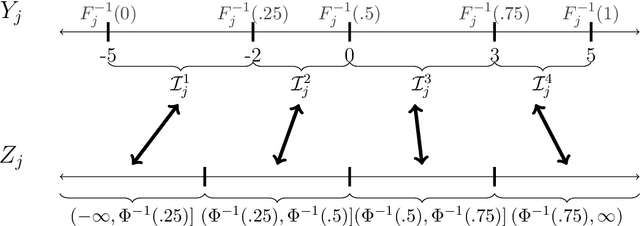
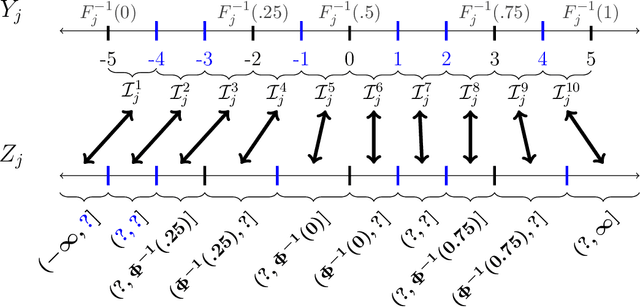
We present an approach for modeling and imputation of nonignorable missing data under Gaussian copulas. The analyst posits a set of quantiles of the marginal distributions of the study variables, for example, reflecting information from external data sources or elicited expert opinion. When these quantiles are accurately specified, we prove it is possible to consistently estimate the copula correlation and perform multiple imputation in the presence of nonignorable missing data. We develop algorithms for estimation and imputation that are computationally efficient, which we evaluate in simulation studies of multiple imputation inferences. We apply the model to analyze associations between lead exposure levels and end-of-grade test scores for 170,000 students in North Carolina. These measurements are not missing at random, as children deemed at-risk for high lead exposure are more likely to be measured. We construct plausible marginal quantiles for lead exposure using national statistics provided by the Centers for Disease Control and Prevention. Complete cases and missing at random analyses appear to underestimate the relationships between certain variables and end-of-grade test scores, while multiple imputation inferences under our model support stronger adverse associations between lead exposure and educational outcomes.