José Alonso Ybanez Zepeda
Geometric Proxies for Live RGB-D Stream Enhancement and Consolidation
Jan 21, 2020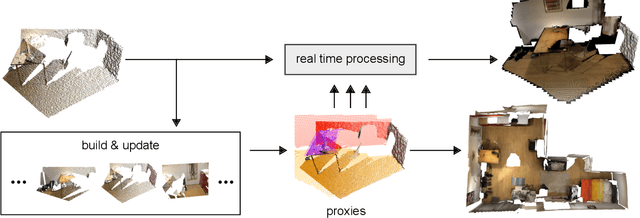
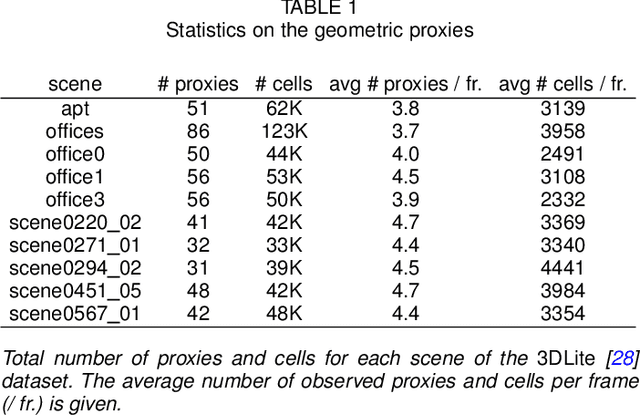


Abstract:We propose a geometric superstructure for unified real-time processing of RGB-D data. Modern RGB-D sensors are widely used for indoor 3D capture, with applications ranging from modeling to robotics, through augmented reality. Nevertheless, their use is limited by their low resolution, with frames often corrupted with noise, missing data and temporal inconsistencies. Our approach consists in generating and updating through time a single set of compact local statistics parameterized over detected geometric proxies, which are fed from raw RGB-D data. Our proxies provide several processing primitives, which improve the quality of the RGB-D stream on the fly or lighten further operations. Experimental results confirm that our lightweight analysis framework copes well with embedded execution as well as moderate memory and computational capabilities compared to state-of-the-art methods. Processing RGB-D data with our proxies allows noise and temporal flickering removal, hole filling and resampling. As a substitute of the observed scene, our proxies can additionally be applied to compression and scene reconstruction. We present experiments performed with our framework in indoor scenes of different natures within a recent open RGB-D dataset.
Plane Pair Matching for Efficient 3D View Registration
Jan 20, 2020
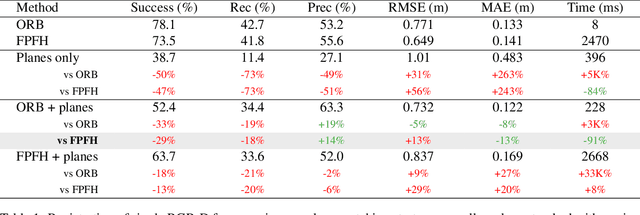


Abstract:We present a novel method to estimate the motion matrix between overlapping pairs of 3D views in the context of indoor scenes. We use the Manhattan world assumption to introduce lightweight geometric constraints under the form of planes into the problem, which reduces complexity by taking into account the structure of the scene. In particular, we define a stochastic framework to categorize planes as vertical or horizontal and parallel or non-parallel. We leverage this classification to match pairs of planes in overlapping views with point-of-view agnostic structural metrics. We propose to split the motion computation using the classification and estimate separately the rotation and translation of the sensor, using a quadric minimizer. We validate our approach on a toy example and present quantitative experiments on a public RGB-D dataset, comparing against recent state-of-the-art methods. Our evaluation shows that planar constraints only add low computational overhead while improving results in precision when applied after a prior coarse estimate. We conclude by giving hints towards extensions and improvements of current results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge