The Amenability Framework: Rethinking Causal Ordering Without Estimating Causal Effects

Who should we prioritize for intervention when we cannot estimate intervention effects? In many applied domains (e.g., advertising, customer retention, and behavioral nudging) prioritization is guided by predictive models that estimate outcome probabilities rather than causal effects. This paper investigates when these predictions (scores) can effectively rank individuals by their intervention effects, particularly when direct effect estimation is infeasible or unreliable. We propose a conceptual framework based on amenability: an individual's latent proclivity to be influenced by an intervention. We then formalize conditions under which predictive scores serve as effective proxies for amenability. These conditions justify using non-causal scores for intervention prioritization, even when the scores do not directly estimate effects. We further show that, under plausible assumptions, predictive models can outperform causal effect estimators in ranking individuals by intervention effects. Empirical evidence from an advertising context supports our theoretical findings, demonstrating that predictive modeling can offer a more robust approach to targeting than effect estimation. Our framework suggests a shift in focus, from estimating effects to inferring who is amenable, as a practical and theoretically grounded strategy for prioritizing interventions in resource-constrained environments.

Deep Kernel Posterior Learning under Infinite Variance Prior Weights

Neal (1996) proved that infinitely wide shallow Bayesian neural networks (BNN) converge to Gaussian processes (GP), when the network weights have bounded prior variance. Cho & Saul (2009) provided a useful recursive formula for deep kernel processes for relating the covariance kernel of each layer to the layer immediately below. Moreover, they worked out the form of the layer-wise covariance kernel in an explicit manner for several common activation functions. Recent works, including Aitchison et al. (2021), have highlighted that the covariance kernels obtained in this manner are deterministic and hence, precludes any possibility of representation learning, which amounts to learning a non-degenerate posterior of a random kernel given the data. To address this, they propose adding artificial noise to the kernel to retain stochasticity, and develop deep kernel inverse Wishart processes. Nonetheless, this artificial noise injection could be critiqued in that it would not naturally emerge in a classic BNN architecture under an infinite-width limit. To address this, we show that a Bayesian deep neural network, where each layer width approaches infinity, and all network weights are elliptically distributed with infinite variance, converges to a process with $\alpha$-stable marginals in each layer that has a conditionally Gaussian representation. These conditional random covariance kernels could be recursively linked in the manner of Cho & Saul (2009), even though marginally the process exhibits stable behavior, and hence covariances are not even necessarily defined. We also provide useful generalizations of the recent results of Lor\'ia & Bhadra (2024) on shallow networks to multi-layer networks, and remedy the computational burden of their approach. The computational and statistical benefits over competing approaches stand out in simulations and in demonstrations on benchmark data sets.

Posterior Inference on Infinitely Wide Bayesian Neural Networks under Weights with Unbounded Variance

From the classical and influential works of Neal (1996), it is known that the infinite width scaling limit of a Bayesian neural network with one hidden layer is a Gaussian process, \emph{when the network weights have bounded prior variance}. Neal's result has been extended to networks with multiple hidden layers and to convolutional neural networks, also with Gaussian process scaling limits. The tractable properties of Gaussian processes then allow straightforward posterior inference and uncertainty quantification, considerably simplifying the study of the limit process compared to a network of finite width. Neural network weights with unbounded variance, however, pose unique challenges. In this case, the classical central limit theorem breaks down and it is well known that the scaling limit is an $\alpha$-stable process under suitable conditions. However, current literature is primarily limited to forward simulations under these processes and the problem of posterior inference under such a scaling limit remains largely unaddressed, unlike in the Gaussian process case. To this end, our contribution is an interpretable and computationally efficient procedure for posterior inference, using a \emph{conditionally Gaussian} representation, that then allows full use of the Gaussian process machinery for tractable posterior inference and uncertainty quantification in the non-Gaussian regime.

Learning the Ranking of Causal Effects with Confounded Data

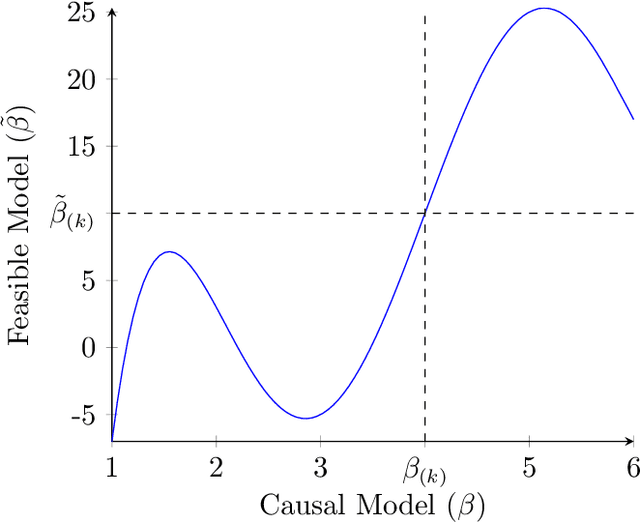
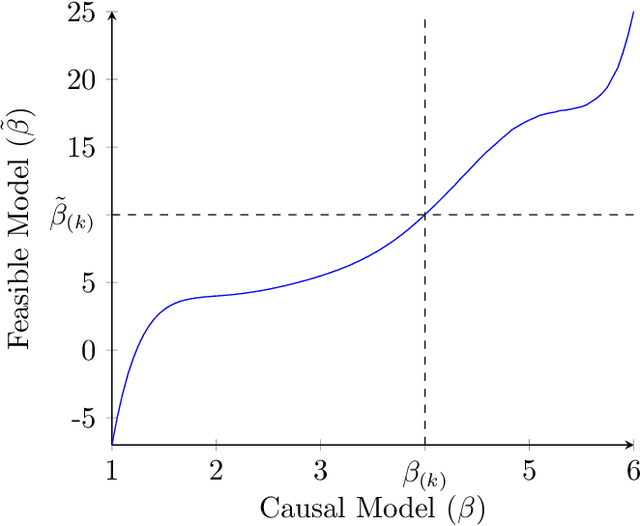
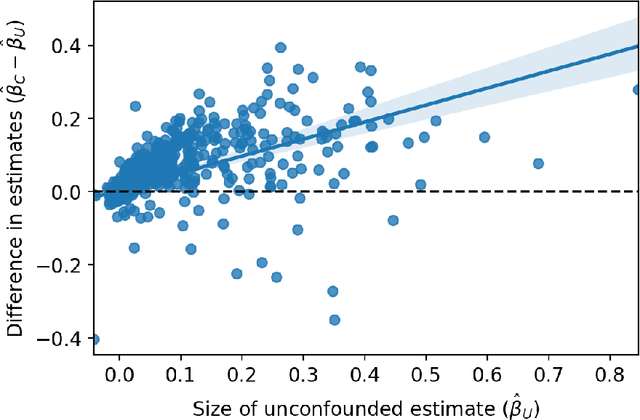
Decision makers often want to identify the individuals for whom some intervention or treatment will be most effective in order to decide who to treat. In such cases, decision makers would ideally like to rank potential recipients of the treatment according to their individual causal effects. However, the historical data available to estimate the causal effects could be confounded, and as a result, accurately estimating the effects could be impossible. We propose a new and less restrictive assumption about historical data, called the ranking preservation assumption (RPA), under which the ranking of the individual effects can be consistently estimated even if the effects themselves cannot be accurately estimated. Importantly, we find that confounding can be helpful for the estimation of the causal-effect ranking when the confounding bias is larger for individuals with larger causal effects, and that even when this is not the case, any detrimental impact of confounding can be corrected with larger training data when the RPA is met. We then analytically show that the RPA can be met in a variety of scenarios, including common business applications such as online advertising and customer retention. We support this finding with an empirical example in the context of online advertising. The example also shows how to evaluate the decision making of a confounded model in practice. The main takeaway is that what might traditionally be considered "good" data for causal estimation (i.e., unconfounded data) may not be necessary to make good causal decisions, so treatment assignment methods may work better than we give them credit for in the presence of confounding.