Exploring the Limits of Fine-grained LLM-based Physics Inference via Premise Removal Interventions

Language models can hallucinate when performing complex and detailed mathematical reasoning. Physics provides a rich domain for assessing mathematical reasoning capabilities where physical context imbues the use of symbols which needs to satisfy complex semantics (\textit{e.g.,} units, tensorial order), leading to instances where inference may be algebraically coherent, yet unphysical. In this work, we assess the ability of Language Models (LMs) to perform fine-grained mathematical and physical reasoning using a curated dataset encompassing multiple notations and Physics subdomains. We improve zero-shot scores using synthetic in-context examples, and demonstrate non-linear degradation of derivation quality with perturbation strength via the progressive omission of supporting premises. We find that the models' mathematical reasoning is not physics-informed in this setting, where physical context is predominantly ignored in favour of reverse-engineering solutions.

Multi-Operational Mathematical Derivations in Latent Space

This paper investigates the possibility of approximating multiple mathematical operations in latent space for expression derivation. To this end, we introduce different multi-operational representation paradigms, modelling mathematical operations as explicit geometric transformations. By leveraging a symbolic engine, we construct a large-scale dataset comprising 1.7M derivation steps stemming from 61K premises and 6 operators, analysing the properties of each paradigm when instantiated with state-of-the-art neural encoders. Specifically, we investigate how different encoding mechanisms can approximate equational reasoning in latent space, exploring the trade-off between learning different operators and specialising within single operations, as well as the ability to support multi-step derivations and out-of-distribution generalisation. Our empirical analysis reveals that the multi-operational paradigm is crucial for disentangling different operators, while discriminating the conclusions for a single operation is achievable in the original expression encoder. Moreover, we show that architectural choices can heavily affect the training dynamics, structural organisation, and generalisation of the latent space, resulting in significant variations across paradigms and classes of encoders.

Generating Mathematical Derivations with Large Language Models

The derivation of mathematical results in specialised fields, using Large Language Models (LLMs), is an emerging research direction that can help identify models' limitations, and potentially support mathematical discovery. In this paper, we leverage a symbolic engine to generate derivations of equations at scale, and investigate the capabilities of LLMs when deriving goal equations from premises. Specifically, we employ in-context learning for GPT and fine-tune a range of T5 models to compare the robustness and generalisation of pre-training strategies to specialised models. Empirical results show that fine-tuned FLAN-T5-large (MathT5) outperforms GPT models on all static and out-of-distribution test sets in conventional scores. However, an in-depth analysis reveals that the fine-tuned models are more sensitive to perturbations involving unseen symbols and (to a lesser extent) changes to equation structure. In addition, we analyse 1.7K equations, and over 200 derivations, to highlight common reasoning errors such as the inclusion of incorrect, irrelevant, and redundant equations. Finally, we explore the suitability of existing metrics for evaluating mathematical derivations and find evidence that, while they can capture general properties such as sensitivity to perturbations, they fail to highlight fine-grained reasoning errors and essential differences between models. Overall, this work demonstrates that training models on synthetic data may improve their math capabilities beyond much larger LLMs, but current metrics are not appropriately assessing the quality of generated mathematical text.

A Symbolic Framework for Systematic Evaluation of Mathematical Reasoning with Transformers

Whether Transformers can learn to apply symbolic rules and generalise to out-of-distribution examples is an open research question. In this paper, we devise a data generation method for producing intricate mathematical derivations, and systematically perturb them with respect to syntax, structure, and semantics. Our task-agnostic approach generates equations, annotations, and inter-equation dependencies, employing symbolic algebra for scalable data production and augmentation. We then instantiate a general experimental framework on next-equation prediction, assessing systematic mathematical reasoning and generalisation of Transformer encoders on a total of 200K examples. The experiments reveal that perturbations heavily affect performance and can reduce F1 scores of $97\%$ to below $17\%$, suggesting that inference is dominated by surface-level patterns unrelated to a deeper understanding of mathematical operators. These findings underscore the importance of rigorous, large-scale evaluation frameworks for revealing fundamental limitations of existing models.

A Survey in Mathematical Language Processing

Informal mathematical text underpins real-world quantitative reasoning and communication. Developing sophisticated methods of retrieval and abstraction from this dual modality is crucial in the pursuit of the vision of automating discovery in quantitative science and mathematics. We track the development of informal mathematical language processing approaches across five strategic sub-areas in recent years, highlighting the prevailing successful methodological elements along with existing limitations.

PhysNLU: A Language Resource for Evaluating Natural Language Understanding and Explanation Coherence in Physics

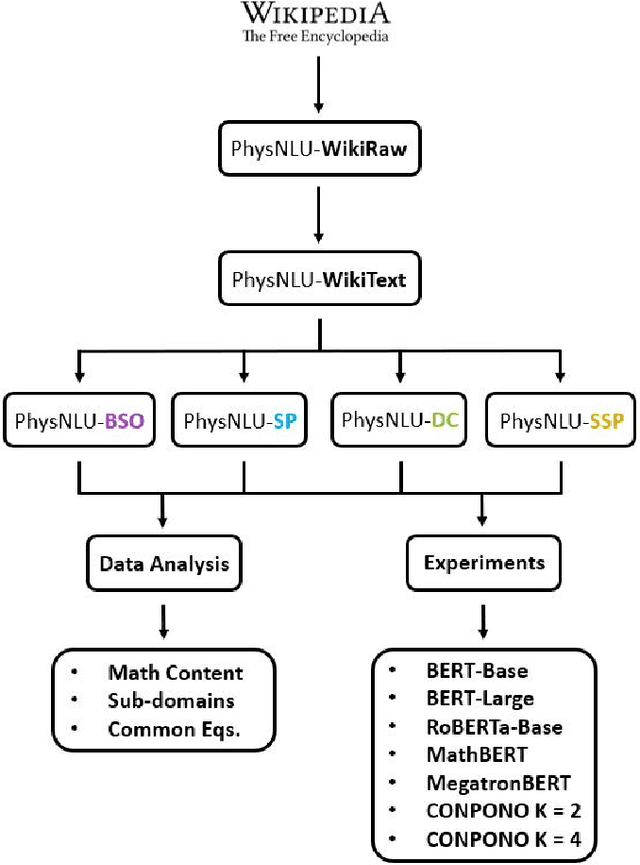
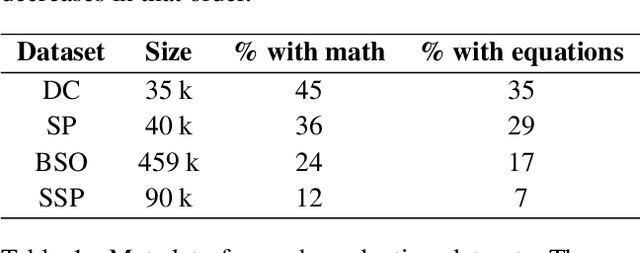
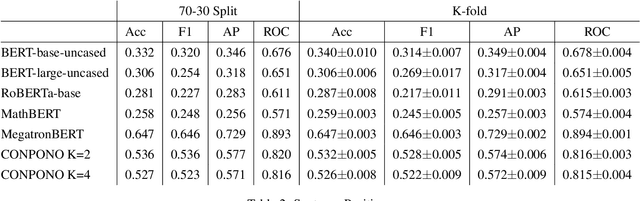
In order for language models to aid physics research, they must first encode representations of mathematical and natural language discourse which lead to coherent explanations, with correct ordering and relevance of statements. We present a collection of datasets developed to evaluate the performance of language models in this regard, which measure capabilities with respect to sentence ordering, position, section prediction, and discourse coherence. Analysis of the data reveals equations and sub-disciplines which are most common in physics discourse, as well as the sentence-level frequency of equations and expressions. We present baselines which demonstrate how contemporary language models are challenged by coherence related tasks in physics, even when trained on mathematical natural language objectives.

Similarity-Based Equational Inference in Physics

Derivation in physics, in the form of derivation reconstruction of published results, is expensive and difficult to automate, not least because the use of mathematics by physicists is less formal than that of mathematicians. Following demand for informal mathematical datasets, we describe a dataset creation method where we consider a derivation agent as a finite state machine which exists in equational states represented by strings, where transitions can occur through a combination of string operations that mimic mathematics, and defined computer algebra operations. We present the novel dataset PhysAI-DS1 generated by this method, which consists of a curated derivation of a contemporary condensed matter physics result reconstructed using a computer algebra system. We define an equation reconstruction task based on formulating derivation segments as basic units of non-trivial state sequences, with the goal of reconstructing an unknown intermediate state equivalent to one-hop inference, extensible to the multi-hop case. We present a symbolic similarity-based heuristic approach to solve an equation reconstruction task on the PhysAI-DS1 dataset, which employs a set of actions, a knowledge base of symbols and equations, and a computer algebra system, to reconstruct an unknown intermediate state within a sequence of three equational states, grouped together as a derivation unit. Informal derivation comprehension of contemporary results is an important step towards the comprehension and automation of modern physics reasoners.