Fitting Laplacian Regularized Stratified Gaussian Models

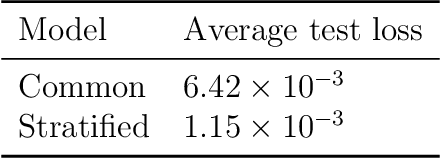
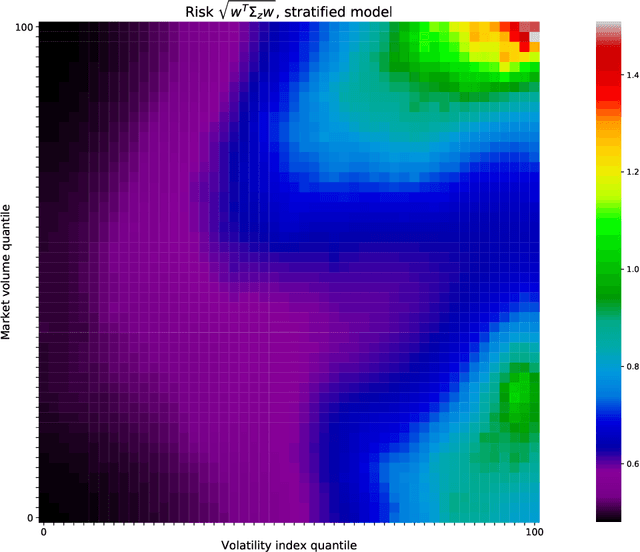
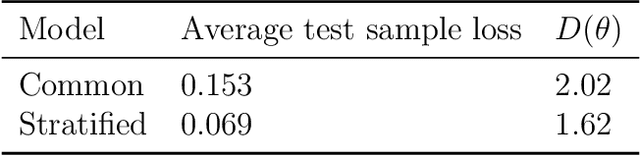
We consider the problem of jointly estimating multiple related zero-mean Gaussian distributions from data. We propose to jointly estimate these covariance matrices using Laplacian regularized stratified model fitting, which includes loss and regularization terms for each covariance matrix, and also a term that encourages the different covariances matrices to be close. This method `borrows strength' from the neighboring covariances, to improve its estimate. With well chosen hyper-parameters, such models can perform very well, especially in the low data regime. We propose a distributed method that scales to large problems, and illustrate the efficacy of the method with examples in finance, radar signal processing, and weather forecasting.

Eigen-Stratified Models

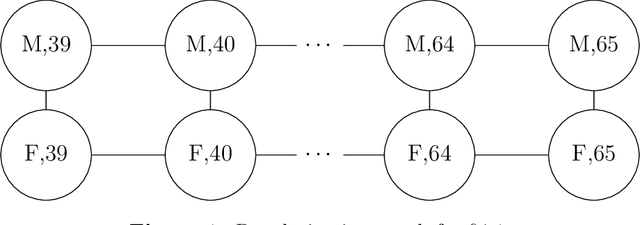
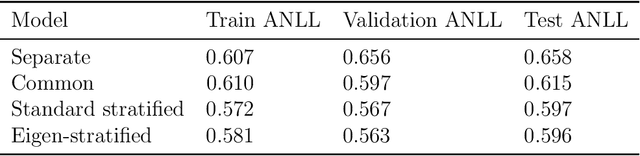
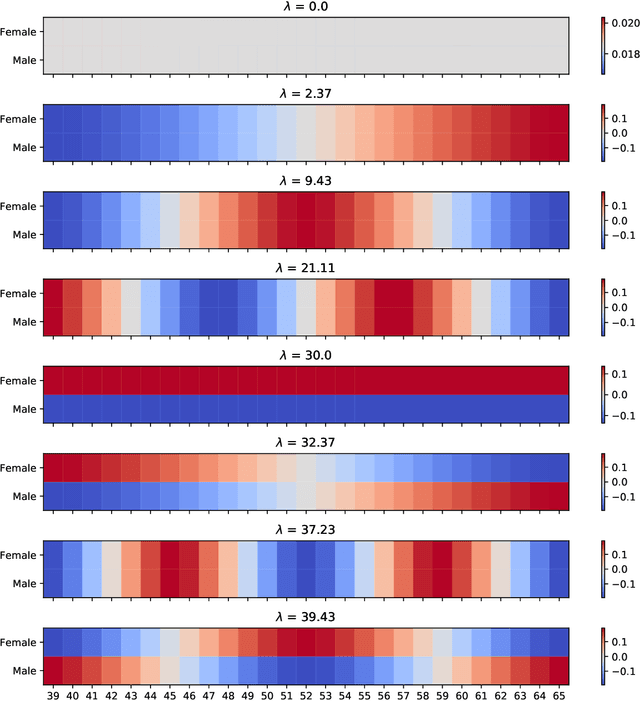
Stratified models depend in an arbitrary way on a selected categorical feature that takes $K$ values, and depend linearly on the other $n$ features. Laplacian regularization with respect to a graph on the feature values can greatly improve the performance of a stratified model, especially in the low-data regime. A significant issue with Laplacian-regularized stratified models is that the model is $K$ times the size of the base model, which can be quite large. We address this issue by formulating eigen-stratifed models, which are stratified models with an additional constraint that the model parameters are linear combinations of some modest number $m$ of bottom eigenvectors of the graph Laplacian, i.e., those associated with the $m$ smallest eigenvalues. With eigen-stratified models, we only need to store the $m$ bottom eigenvectors and the corresponding coefficients as the stratified model parameters. This leads to a reduction, sometimes large, of model size when $m \leq n$ and $m \ll K$. In some cases, the additional regularization implicit in eigen-stratified models can improve out-of-sample performance over standard Laplacian regularized stratified models.

A Distributed Method for Fitting Laplacian Regularized Stratified Models

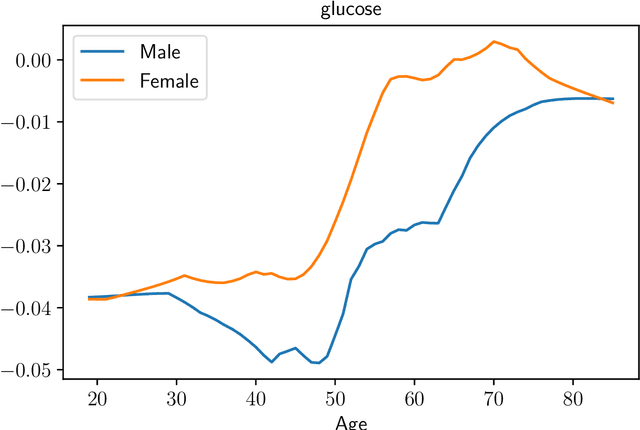
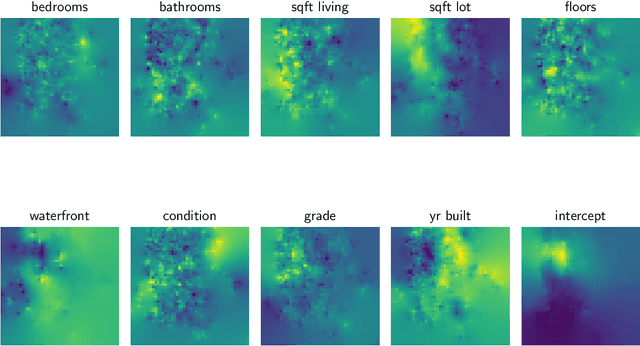
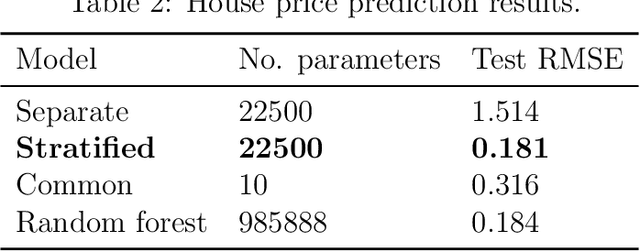
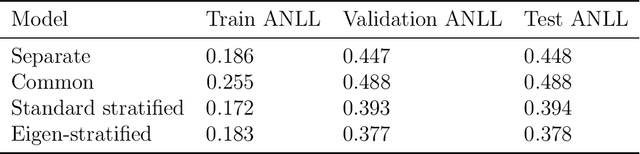
Stratified models are models that depend in an arbitrary way on a set of selected categorical features, and depend linearly on the other features. In a basic and traditional formulation a separate model is fit for each value of the categorical feature, using only the data that has the specific categorical value. To this formulation we add Laplacian regularization, which encourages the model parameters for neighboring categorical values to be similar. Laplacian regularization allows us to specify one or more weighted graphs on the stratification feature values. For example, stratifying over the days of the week, we can specify that the Sunday model parameter should be close to the Saturday and Monday model parameters. The regularization improves the performance of the model over the traditional stratified model, since the model for each value of the categorical `borrows strength' from its neighbors. In particular, it produces a model even for categorical values that did not appear in the training data set. We propose an efficient distributed method for fitting stratified models, based on the alternating direction method of multipliers (ADMM). When the fitting loss functions are convex, the stratified model fitting problem is convex, and our method computes the global minimizer of the loss plus regularization; in other cases it computes a local minimizer. The method is very efficient, and naturally scales to large data sets or numbers of stratified feature values. We illustrate our method with a variety of examples.