Eigen-Stratified Models
Paper and Code
Jan 27, 2020
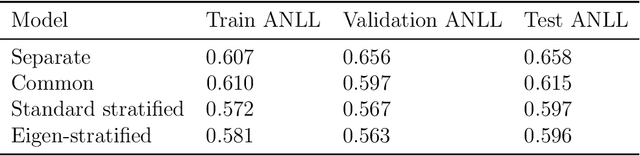
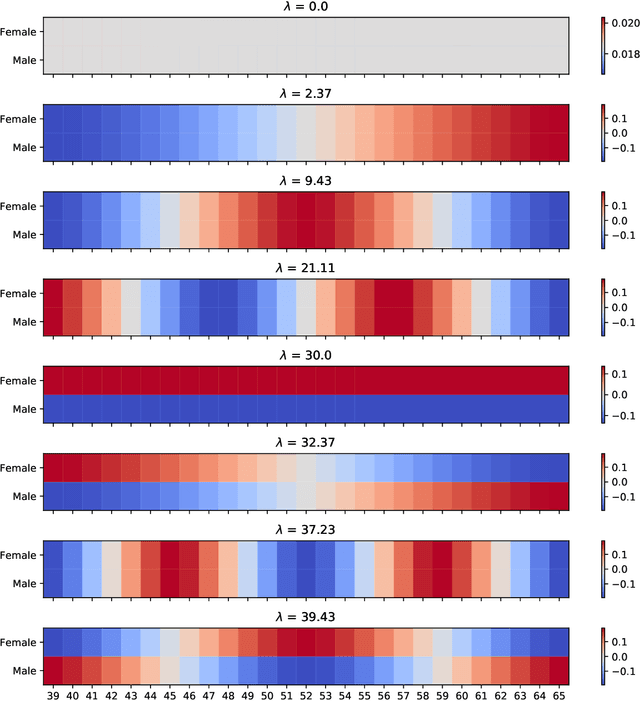
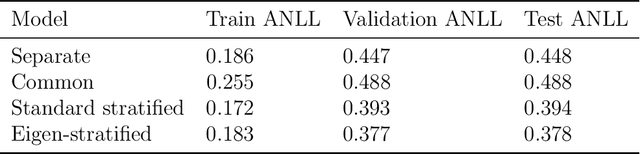
Stratified models depend in an arbitrary way on a selected categorical feature that takes $K$ values, and depend linearly on the other $n$ features. Laplacian regularization with respect to a graph on the feature values can greatly improve the performance of a stratified model, especially in the low-data regime. A significant issue with Laplacian-regularized stratified models is that the model is $K$ times the size of the base model, which can be quite large. We address this issue by formulating eigen-stratifed models, which are stratified models with an additional constraint that the model parameters are linear combinations of some modest number $m$ of bottom eigenvectors of the graph Laplacian, i.e., those associated with the $m$ smallest eigenvalues. With eigen-stratified models, we only need to store the $m$ bottom eigenvectors and the corresponding coefficients as the stratified model parameters. This leads to a reduction, sometimes large, of model size when $m \leq n$ and $m \ll K$. In some cases, the additional regularization implicit in eigen-stratified models can improve out-of-sample performance over standard Laplacian regularized stratified models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge