SplashNet: Split-and-Share Encoders for Accurate and Efficient Typing with Surface Electromyography

Surface electromyography (sEMG) at the wrists could enable natural, keyboard-free text entry, yet the state-of-the-art emg2qwerty baseline still misrecognizes $51.8\%$ of characters in the zero-shot setting on unseen users and $7.0\%$ after user-specific fine-tuning. We trace many of these errors to mismatched cross-user signal statistics, fragile reliance on high-order feature dependencies, and the absence of architectural inductive biases aligned with the bilateral nature of typing. To address these issues, we introduce three simple modifications: (i) Rolling Time Normalization, which adaptively aligns input distributions across users; (ii) Aggressive Channel Masking, which encourages reliance on low-order feature combinations more likely to generalize across users; and (iii) a Split-and-Share encoder that processes each hand independently with weight-shared streams to reflect the bilateral symmetry of the neuromuscular system. Combined with a five-fold reduction in spectral resolution ($33\!\rightarrow\!6$ frequency bands), these components yield a compact Split-and-Share model, SplashNet-mini, which uses only $\tfrac14$ the parameters and $0.6\times$ the FLOPs of the baseline while reducing character-error rate (CER) to $36.4\%$ zero-shot and $5.9\%$ after fine-tuning. An upscaled variant, SplashNet ($\tfrac12$ the parameters, $1.15\times$ the FLOPs of the baseline), further lowers error to $35.7\%$ and $5.5\%$, representing relative improvements of $31\%$ and $21\%$ in the zero-shot and fine-tuned settings, respectively. SplashNet therefore establishes a new state of the art without requiring additional data.

Gacs-Korner Common Information Variational Autoencoder

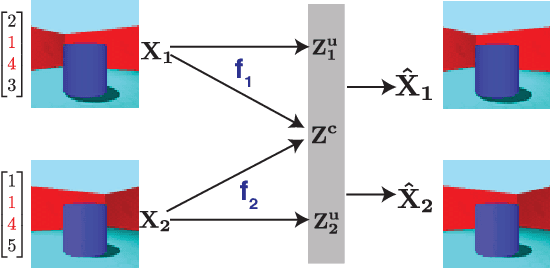
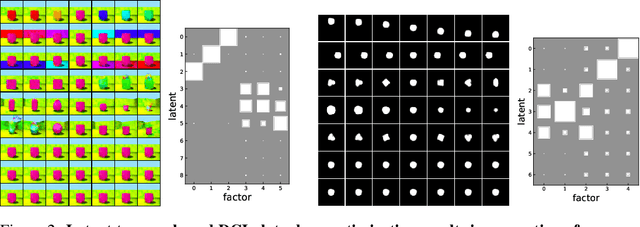
We propose a notion of common information that allows one to quantify and separate the information that is shared between two random variables from the information that is unique to each. Our notion of common information is a variational relaxation of the G\'acs-K\"orner common information, which we recover as a special case, but is more amenable to optimization and can be approximated empirically using samples from the underlying distribution. We then provide a method to partition and quantify the common and unique information using a simple modification of a traditional variational auto-encoder. Empirically, we demonstrate that our formulation allows us to learn semantically meaningful common and unique factors of variation even on high-dimensional data such as images and videos. Moreover, on datasets where ground-truth latent factors are known, we show that we can accurately quantify the common information between the random variables. Additionally, we show that the auto-encoder that we learn recovers semantically meaningful disentangled factors of variation, even though we do not explicitly optimize for it.