Training Large Neural Networks With Low-Dimensional Error Feedback

Training deep neural networks typically relies on backpropagating high dimensional error signals a computationally intensive process with little evidence supporting its implementation in the brain. However, since most tasks involve low-dimensional outputs, we propose that low-dimensional error signals may suffice for effective learning. To test this hypothesis, we introduce a novel local learning rule based on Feedback Alignment that leverages indirect, low-dimensional error feedback to train large networks. Our method decouples the backward pass from the forward pass, enabling precise control over error signal dimensionality while maintaining high-dimensional representations. We begin with a detailed theoretical derivation for linear networks, which forms the foundation of our learning framework, and extend our approach to nonlinear, convolutional, and transformer architectures. Remarkably, we demonstrate that even minimal error dimensionality on the order of the task dimensionality can achieve performance matching that of traditional backpropagation. Furthermore, our rule enables efficient training of convolutional networks, which have previously been resistant to Feedback Alignment methods, with minimal error. This breakthrough not only paves the way toward more biologically accurate models of learning but also challenges the conventional reliance on high-dimensional gradient signals in neural network training. Our findings suggest that low-dimensional error signals can be as effective as high-dimensional ones, prompting a reevaluation of gradient-based learning in high-dimensional systems. Ultimately, our work offers a fresh perspective on neural network optimization and contributes to understanding learning mechanisms in both artificial and biological systems.

Predictive coding in balanced neural networks with noise, chaos and delays

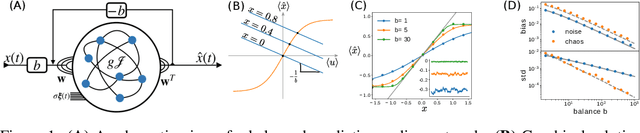
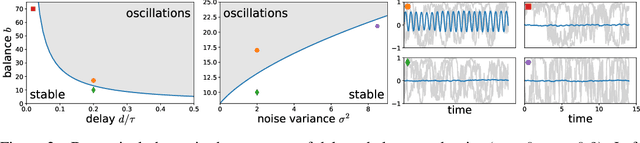
Biological neural networks face a formidable task: performing reliable computations in the face of intrinsic stochasticity in individual neurons, imprecisely specified synaptic connectivity, and nonnegligible delays in synaptic transmission. A common approach to combatting such biological heterogeneity involves averaging over large redundant networks of $N$ neurons resulting in coding errors that decrease classically as $1/\sqrt{N}$. Recent work demonstrated a novel mechanism whereby recurrent spiking networks could efficiently encode dynamic stimuli, achieving a superclassical scaling in which coding errors decrease as $1/N$. This specific mechanism involved two key ideas: predictive coding, and a tight balance, or cancellation between strong feedforward inputs and strong recurrent feedback. However, the theoretical principles governing the efficacy of balanced predictive coding and its robustness to noise, synaptic weight heterogeneity and communication delays remain poorly understood. To discover such principles, we introduce an analytically tractable model of balanced predictive coding, in which the degree of balance and the degree of weight disorder can be dissociated unlike in previous balanced network models, and we develop a mean field theory of coding accuracy. Overall, our work provides and solves a general theoretical framework for dissecting the differential contributions neural noise, synaptic disorder, chaos, synaptic delays, and balance to the fidelity of predictive neural codes, reveals the fundamental role that balance plays in achieving superclassical scaling, and unifies previously disparate models in theoretical neuroscience.

Statistical mechanics of low-rank tensor decomposition

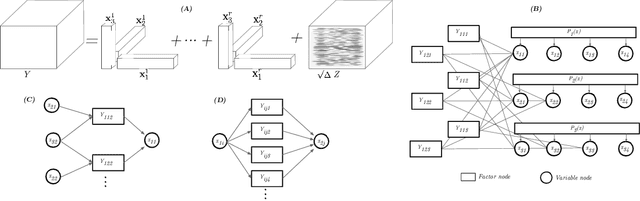
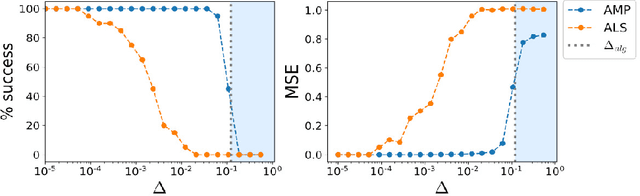
Often, large, high dimensional datasets collected across multiple modalities can be organized as a higher order tensor. Low-rank tensor decomposition then arises as a powerful and widely used tool to discover simple low dimensional structures underlying such data. However, we currently lack a theoretical understanding of the algorithmic behavior of low-rank tensor decompositions. We derive Bayesian approximate message passing (AMP) algorithms for recovering arbitrarily shaped low-rank tensors buried within noise, and we employ dynamic mean field theory to precisely characterize their performance. Our theory reveals the existence of phase transitions between easy, hard and impossible inference regimes, and displays an excellent match with simulations. Moreover, it reveals several qualitative surprises compared to the behavior of symmetric, cubic tensor decomposition. Finally, we compare our AMP algorithm to the most commonly used algorithm, alternating least squares (ALS), and demonstrate that AMP significantly outperforms ALS in the presence of noise.