IAEmu: Learning Galaxy Intrinsic Alignment Correlations

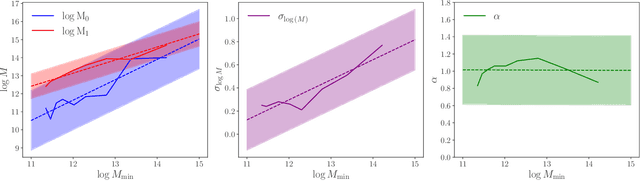
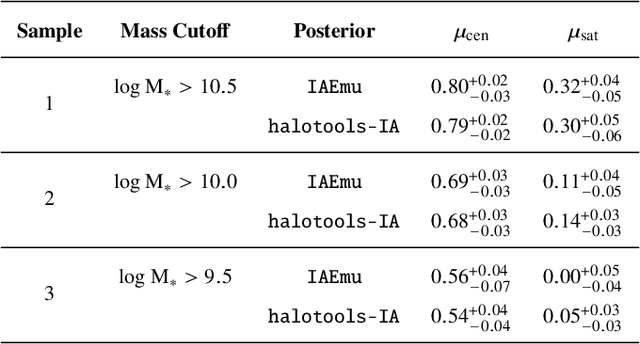
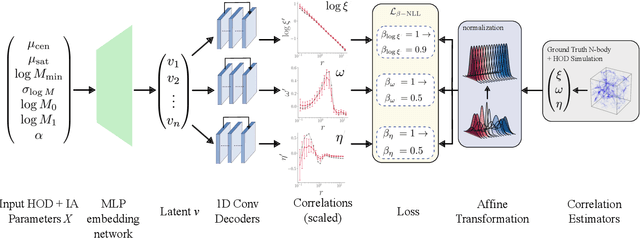
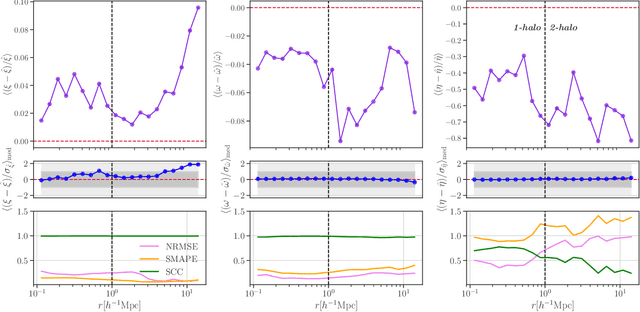
The intrinsic alignments (IA) of galaxies, a key contaminant in weak lensing analyses, arise from correlations in galaxy shapes driven by tidal interactions and galaxy formation processes. Accurate IA modeling is essential for robust cosmological inference, but current approaches rely on perturbative methods that break down on nonlinear scales or on expensive simulations. We introduce IAEmu, a neural network-based emulator that predicts the galaxy position-position ($\xi$), position-orientation ($\omega$), and orientation-orientation ($\eta$) correlation functions and their uncertainties using mock catalogs based on the halo occupation distribution (HOD) framework. Compared to simulations, IAEmu achieves ~3% average error for $\xi$ and ~5% for $\omega$, while capturing the stochasticity of $\eta$ without overfitting. The emulator provides both aleatoric and epistemic uncertainties, helping identify regions where predictions may be less reliable. We also demonstrate generalization to non-HOD alignment signals by fitting to IllustrisTNG hydrodynamical simulation data. As a fully differentiable neural network, IAEmu enables $\sim$10,000$\times$ speed-ups in mapping HOD parameters to correlation functions on GPUs, compared to CPU-based simulations. This acceleration facilitates inverse modeling via gradient-based sampling, making IAEmu a powerful surrogate model for galaxy bias and IA studies with direct applications to Stage IV weak lensing surveys.

Learning Galaxy Intrinsic Alignment Correlations

The intrinsic alignments (IA) of galaxies, regarded as a contaminant in weak lensing analyses, represents the correlation of galaxy shapes due to gravitational tidal interactions and galaxy formation processes. As such, understanding IA is paramount for accurate cosmological inferences from weak lensing surveys; however, one limitation to our understanding and mitigation of IA is expensive simulation-based modeling. In this work, we present a deep learning approach to emulate galaxy position-position ($\xi$), position-orientation ($\omega$), and orientation-orientation ($\eta$) correlation function measurements and uncertainties from halo occupation distribution-based mock galaxy catalogs. We find strong Pearson correlation values with the model across all three correlation functions and further predict aleatoric uncertainties through a mean-variance estimation training procedure. $\xi(r)$ predictions are generally accurate to $\leq10\%$. Our model also successfully captures the underlying signal of the noisier correlations $\omega(r)$ and $\eta(r)$, although with a lower average accuracy. We find that the model performance is inhibited by the stochasticity of the data, and will benefit from correlations averaged over multiple data realizations. Our code will be made open source upon journal publication.

E(2) Equivariant Neural Networks for Robust Galaxy Morphology Classification

We propose the use of group convolutional neural network architectures (GCNNs) equivariant to the 2D Euclidean group, $E(2)$, for the task of galaxy morphology classification by utilizing symmetries of the data present in galaxy images as an inductive bias in the architecture. We conduct robustness studies by introducing artificial perturbations via Poisson noise insertion and one-pixel adversarial attacks to simulate the effects of limited observational capabilities. We train, validate, and test GCNNs equivariant to discrete subgroups of $E(2)$ - the cyclic and dihedral groups of order $N$ - on the Galaxy10 DECals dataset and find that GCNNs achieve higher classification accuracy and are consistently more robust than their non-equivariant counterparts, with an architecture equivariant to the group $D_{16}$ achieving a $95.52 \pm 0.18\%$ test-set accuracy. We also find that the model loses $<6\%$ accuracy on a $50\%$-noise dataset and all GCNNs are less susceptible to one-pixel perturbations than an identically constructed CNN. Our code is publicly available at https://github.com/snehjp2/GCNNMorphology.