Assessing Differentially Private Variational Autoencoders under Membership Inference

We present an approach to quantify and compare the privacy-accuracy trade-off for differentially private Variational Autoencoders. Our work complements previous work in two aspects. First, we evaluate the the strong reconstruction MI attack against Variational Autoencoders under differential privacy. Second, we address the data scientist's challenge of setting privacy parameter epsilon, which steers the differential privacy strength and thus also the privacy-accuracy trade-off. In our experimental study we consider image and time series data, and three local and central differential privacy mechanisms. We find that the privacy-accuracy trade-offs strongly depend on the dataset and model architecture. We do rarely observe favorable privacy-accuracy trade-off for Variational Autoencoders, and identify a case where LDP outperforms CDP.

Assessing differentially private deep learning with Membership Inference

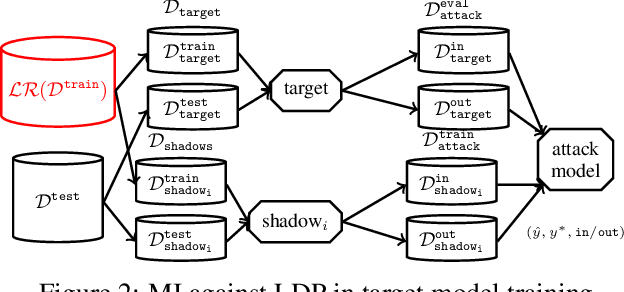
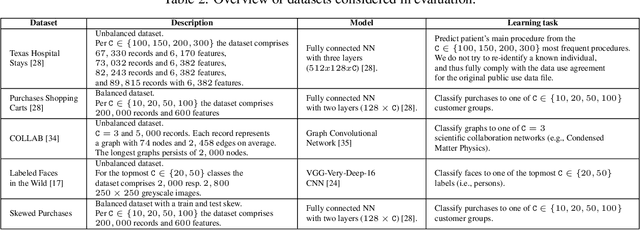
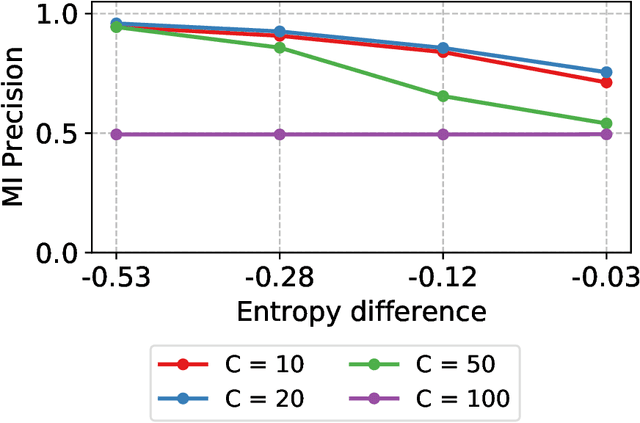
Releasing data in the form of trained neural networks with differential privacy promises meaningful anonymization. However, there is an inherent privacy-accuracy trade-off in differential privacy which is challenging to assess for non-privacy experts. Furthermore, local and central differential privacy mechanisms are available to either anonymize the training data or the learnt neural network, and the privacy parameter $\epsilon$ cannot be used to compare these two mechanisms. We propose to measure privacy through a black-box membership inference attack and compare the privacy-accuracy trade-off for different local and central differential privacy mechanisms. Furthermore, we need to evaluate whether differential privacy is a useful mechanism in practice since differential privacy will especially be used by data scientists if membership inference risk is lowered more than accuracy. We experiment with several datasets and show that neither local differential privacy nor central differential privacy yields a consistently better privacy-accuracy trade-off in all cases. We also show that the relative privacy-accuracy trade-off, instead of strictly declining linearly over $\epsilon$, is only favorable within a small interval. For this purpose we propose $\varphi$, a ratio expressing the relative privacy-accuracy trade-off.