On The Continuous Steering of the Scale of Tight Wavelet Frames

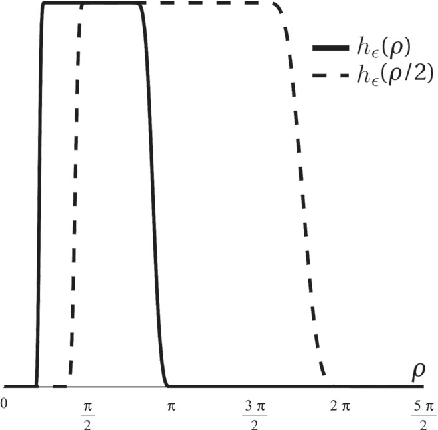
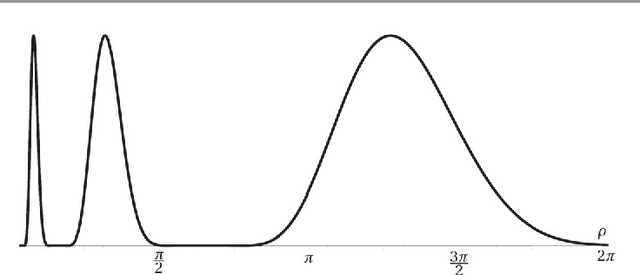
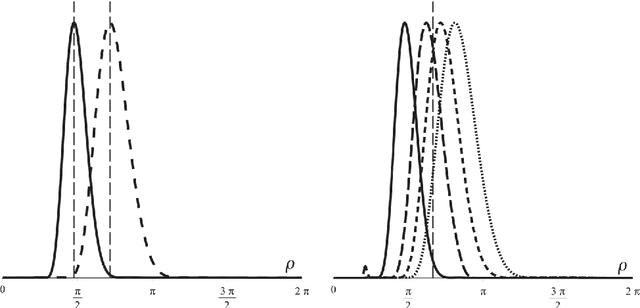
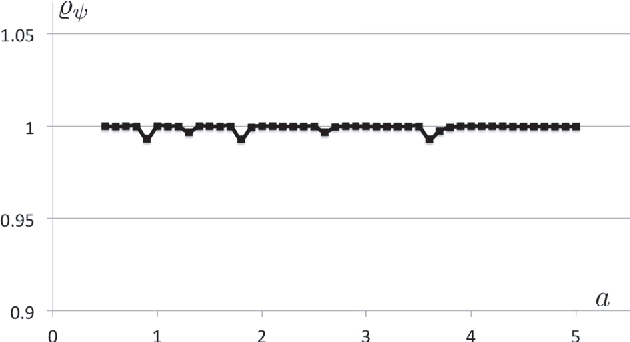
In analogy with steerable wavelets, we present a general construction of adaptable tight wavelet frames, with an emphasis on scaling operations. In particular, the derived wavelets can be "dilated" by a procedure comparable to the operation of steering steerable wavelets. The fundamental aspects of the construction are the same: an admissible collection of Fourier multipliers is used to extend a tight wavelet frame, and the "scale" of the wavelets is adapted by scaling the multipliers. As an application, the proposed wavelets can be used to improve the frequency localization. Importantly, the localized frequency bands specified by this construction can be scaled efficiently using matrix multiplication.

Hessian Schatten-Norm Regularization for Linear Inverse Problems

We introduce a novel family of invariant, convex, and non-quadratic functionals that we employ to derive regularized solutions of ill-posed linear inverse imaging problems. The proposed regularizers involve the Schatten norms of the Hessian matrix, computed at every pixel of the image. They can be viewed as second-order extensions of the popular total-variation (TV) semi-norm since they satisfy the same invariance properties. Meanwhile, by taking advantage of second-order derivatives, they avoid the staircase effect, a common artifact of TV-based reconstructions, and perform well for a wide range of applications. To solve the corresponding optimization problems, we propose an algorithm that is based on a primal-dual formulation. A fundamental ingredient of this algorithm is the projection of matrices onto Schatten norm balls of arbitrary radius. This operation is performed efficiently based on a direct link we provide between vector projections onto $\ell_q$ norm balls and matrix projections onto Schatten norm balls. Finally, we demonstrate the effectiveness of the proposed methods through experimental results on several inverse imaging problems with real and simulated data.