Redeeming Data Science by Decision Modelling

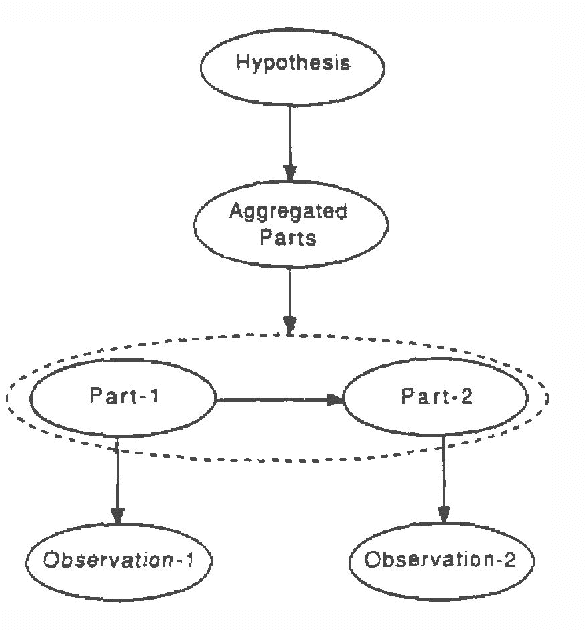
With the explosion of applications of Data Science, the field is has come loose from its foundations. This article argues for a new program of applied research in areas familiar to researchers in Bayesian methods in AI that are needed to ground the practice of Data Science by borrowing from AI techniques for model formulation that we term ``Decision Modelling.'' This article briefly reviews the formulation process as building a causal graphical model, then discusses the process in terms of six principles that comprise \emph{Decision Quality}, a framework from the popular business literature. We claim that any successful applied ML modelling effort must include these six principles. We explain how Decision Modelling combines a conventional machine learning model with an explicit value model. To give a specific example we show how this is done by integrating a model's ROC curve with a utility model.

Hierarchical Bayesian Regression for Multi-Location Sales Transaction Forecasting

The features in many prediction models naturally take the form of a hierarchy. The lower levels represent individuals or events. These units group naturally into locations and intervals or other aggregates, often at multiple levels. Levels of groupings may intersect and join, much as relational database tables do. Besides representing the structure of the data, predictive features in hierarchical models can be assigned to their proper levels. Such models lend themselves to hierarchical Bayes solution methods that ``share'' results of inference between groups by generalizing over the case of individual models for each group versus one model that aggregates all groups into one. In this paper we show our work-in-progress applying a hierarchical Bayesian model to forecast purchases throughout the day at store franchises, with groupings over locations and days of the week. We demonstrate using the \textsf{stan} package on individual sales transaction data collected over the course of a year. We show how this solves the dilemma of having limited data and hence modest accuracy for each day and location, while being able to scale to a large number of locations with improved accuracy.

The structure of Bayes nets for vision recognition

This paper is part of a study whose goal is to show the effciency of using Bayes networks to carry out model based vision calculations. [Binford et al. 1987] Recognition proceeds by drawing up a network model from the object's geometric and functional description that predicts the appearance of an object. Then this network is used to find the object within a photographic image. Many existing and proposed techniques for vision recognition resemble the uncertainty calculations of a Bayes net. In contrast, though, they lack a derivation from first principles, and tend to rely on arbitrary parameters that we hope to avoid by a network model. The connectedness of the network depends on what independence considerations can be identified in the vision problem. Greater independence leads to easier calculations, at the expense of the net's expressiveness. Once this trade-off is made and the structure of the network is determined, it should be possible to tailor a solution technique for it. This paper explores the use of a network with multiply connected paths, drawing on both techniques of belief networks [Pearl 86] and influence diagrams. We then demonstrate how one formulation of a multiply connected network can be solved.

Model-based Influence Diagrams for Machine Vision

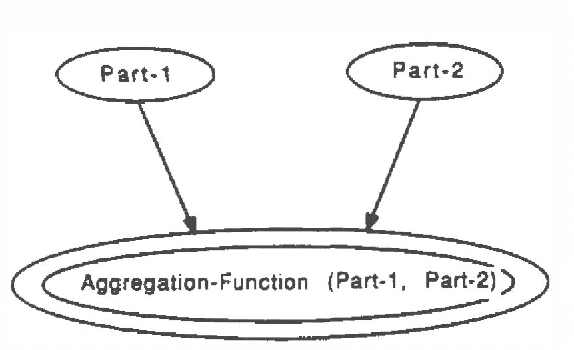
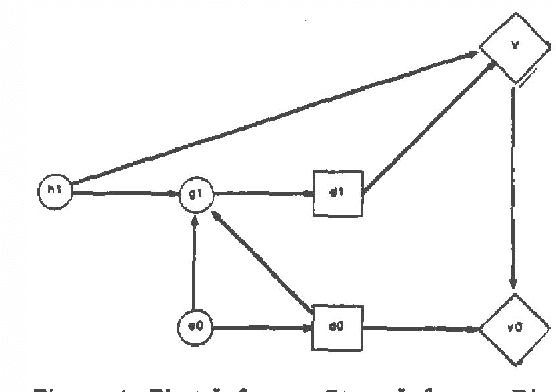
We show an approach to automated control of machine vision systems based on incremental creation and evaluation of a particular family of influence diagrams that represent hypotheses of imagery interpretation and possible subsequent processing decisions. In our approach, model-based machine vision techniques are integrated with hierarchical Bayesian inference to provide a framework for representing and matching instances of objects and relationships in imagery and for accruing probabilities to rank order conflicting scene interpretations. We extend a result of Tatman and Shachter to show that the sequence of processing decisions derived from evaluating the diagrams at each stage is the same as the sequence that would have been derived by evaluating the final influence diagram that contains all random variables created during the run of the vision system.

"Conditional Inter-Causally Independent" Node Distributions, a Property of "Noisy-Or" Models

This paper examines the interdependence generated between two parent nodes with a common instantiated child node, such as two hypotheses sharing common evidence. The relation so generated has been termed "intercausal." It is shown by construction that inter-causal independence is possible for binary distributions at one state of evidence. For such "CICI" distributions, the two measures of inter-causal effect, "multiplicative synergy" and "additive synergy" are equal. The well known "noisy-or" model is an example of such a distribution. This introduces novel semantics for the noisy-or, as a model of the degree of conflict among competing hypotheses of a common observation.

Constraining Influence Diagram Structure by Generative Planning: An Application to the Optimization of Oil Spill Response

This paper works through the optimization of a real world planning problem, with a combination of a generative planning tool and an influence diagram solver. The problem is taken from an existing application in the domain of oil spill emergency response. The planning agent manages constraints that order sets of feasible equipment employment actions. This is mapped at an intermediate level of abstraction onto an influence diagram. In addition, the planner can apply a surveillance operator that determines observability of the state---the unknown trajectory of the oil. The uncertain world state and the objective function properties are part of the influence diagram structure, but not represented in the planning agent domain. By exploiting this structure under the constraints generated by the planning agent, the influence diagram solution complexity simplifies considerably, and an optimum solution to the employment problem based on the objective function is found. Finding this optimum is equivalent to the simultaneous evaluation of a range of plans. This result is an example of bounded optimality, within the limitations of this hybrid generative planner and influence diagram architecture.