Large language model validity via enhanced conformal prediction methods

We develop new conformal inference methods for obtaining validity guarantees on the output of large language models (LLMs). Prior work in conformal language modeling identifies a subset of the text that satisfies a high-probability guarantee of correctness. These methods work by filtering claims from the LLM's original response if a scoring function evaluated on the claim fails to exceed a threshold calibrated via split conformal prediction. Existing methods in this area suffer from two deficiencies. First, the guarantee stated is not conditionally valid. The trustworthiness of the filtering step may vary based on the topic of the response. Second, because the scoring function is imperfect, the filtering step can remove many valuable and accurate claims. We address both of these challenges via two new conformal methods. First, we generalize the conditional conformal procedure of Gibbs et al. (2023) in order to adaptively issue weaker guarantees when they are required to preserve the utility of the output. Second, we show how to systematically improve the quality of the scoring function via a novel algorithm for differentiating through the conditional conformal procedure. We demonstrate the efficacy of our approach on both synthetic and real-world datasets.

Statistical Inference for Fairness Auditing

Before deploying a black-box model in high-stakes problems, it is important to evaluate the model's performance on sensitive subpopulations. For example, in a recidivism prediction task, we may wish to identify demographic groups for which our prediction model has unacceptably high false positive rates or certify that no such groups exist. In this paper, we frame this task, often referred to as "fairness auditing," in terms of multiple hypothesis testing. We show how the bootstrap can be used to simultaneously bound performance disparities over a collection of groups with statistical guarantees. Our methods can be used to flag subpopulations affected by model underperformance, and certify subpopulations for which the model performs adequately. Crucially, our audit is model-agnostic and applicable to nearly any performance metric or group fairness criterion. Our methods also accommodate extremely rich -- even infinite -- collections of subpopulations. Further, we generalize beyond subpopulations by showing how to assess performance over certain distribution shifts. We test the proposed methods on benchmark datasets in predictive inference and algorithmic fairness and find that our audits can provide interpretable and trustworthy guarantees.

Efficient hyperparameter optimization by way of PAC-Bayes bound minimization

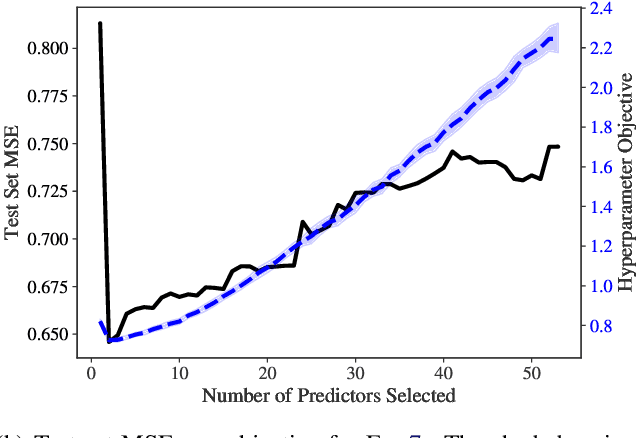
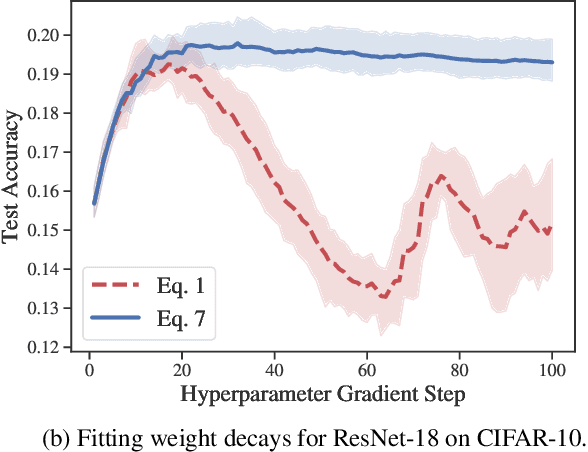
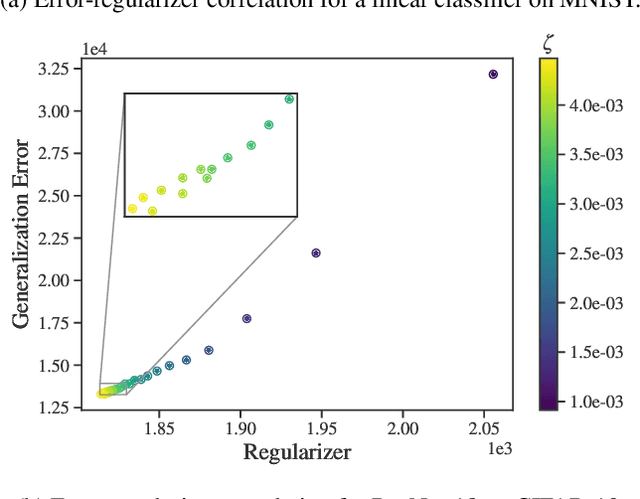
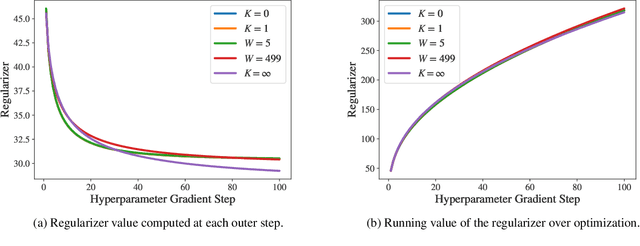
Identifying optimal values for a high-dimensional set of hyperparameters is a problem that has received growing attention given its importance to large-scale machine learning applications such as neural architecture search. Recently developed optimization methods can be used to select thousands or even millions of hyperparameters. Such methods often yield overfit models, however, leading to poor performance on unseen data. We argue that this overfitting results from using the standard hyperparameter optimization objective function. Here we present an alternative objective that is equivalent to a Probably Approximately Correct-Bayes (PAC-Bayes) bound on the expected out-of-sample error. We then devise an efficient gradient-based algorithm to minimize this objective; the proposed method has asymptotic space and time complexity equal to or better than other gradient-based hyperparameter optimization methods. We show that this new method significantly reduces out-of-sample error when applied to hyperparameter optimization problems known to be prone to overfitting.