Speeding up approximate MAP by applying domain knowledge about relevant variables

The MAP problem in Bayesian networks is notoriously intractable, even when approximated. In an earlier paper we introduced the Most Frugal Explanation heuristic approach to solving MAP, by partitioning the set of intermediate variables (neither observed nor part of the MAP variables) into a set of relevant variables, which are marginalized out, and irrelevant variables, which will be assigned a sampled value from their domain. In this study we explore whether knowledge about which variables are relevant for a particular query (i.e., domain knowledge) speeds up computation sufficiently to beat both exact MAP as well as approximate MAP while giving reasonably accurate results. Our results are inconclusive, but also show that this probably depends on the specifics of the MAP query, most prominently the number of MAP variables.

Cancer Subtype Identification through Integrating Inter and Intra Dataset Relationships in Multi-Omics Data

The integration of multi-omics data has emerged as a promising approach for gaining comprehensive insights into complex diseases such as cancer. This paper proposes a novel approach to identify cancer subtypes through the integration of multi-omics data for clustering. The proposed method, named LIDAF utilises affinity matrices based on linear relationships between and within different omics datasets (Linear Inter and Intra Dataset Affinity Fusion (LIDAF)). Canonical Correlation Analysis is in this paper employed to create distance matrices based on Euclidean distances between canonical variates. The distance matrices are converted to affinity matrices and those are fused in a three-step process. The proposed LIDAF addresses the limitations of the existing method resulting in improvement of clustering performance as measured by the Adjusted Rand Index and the Normalized Mutual Information score. Moreover, our proposed LIDAF approach demonstrates a notable enhancement in 50% of the log10 rank p-values obtained from Cox survival analysis, surpassing the performance of the best reported method, highlighting its potential of identifying distinct cancer subtypes.

Bayesian Integration of Information Using Top-Down Modulated WTA Networks

Winner Take All (WTA) circuits a type of Spiking Neural Networks (SNN) have been suggested as facilitating the brain's ability to process information in a Bayesian manner. Research has shown that WTA circuits are capable of approximating hierarchical Bayesian models via Expectation Maximization (EM). So far, research in this direction has focused on bottom up processes. This is contrary to neuroscientific evidence that shows that, besides bottom up processes, top down processes too play a key role in information processing by the human brain. Several functions ascribed to top down processes include direction of attention, adjusting for expectations, facilitation of encoding and recall of learned information, and imagery. This paper explores whether WTA circuits are suitable for further integrating information represented in separate WTA networks. Furthermore, it explores whether, and under what circumstances, top down processes can improve WTA network performance with respect to inference and learning. The results show that WTA circuits are capable of integrating the probabilistic information represented by other WTA networks, and that top down processes can improve a WTA network's inference and learning performance. Notably, it is able to do this according to key neuromorphic principles, making it ideal for low-latency and energy efficient implementation on neuromorphic hardware.

Benchmarking energy consumption and latency for neuromorphic computing in condensed matter and particle physics

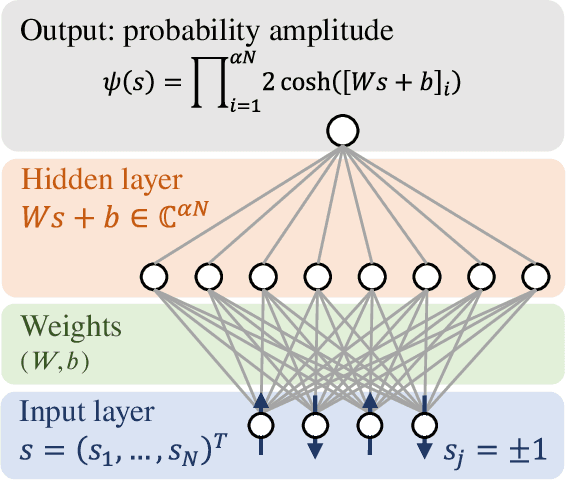
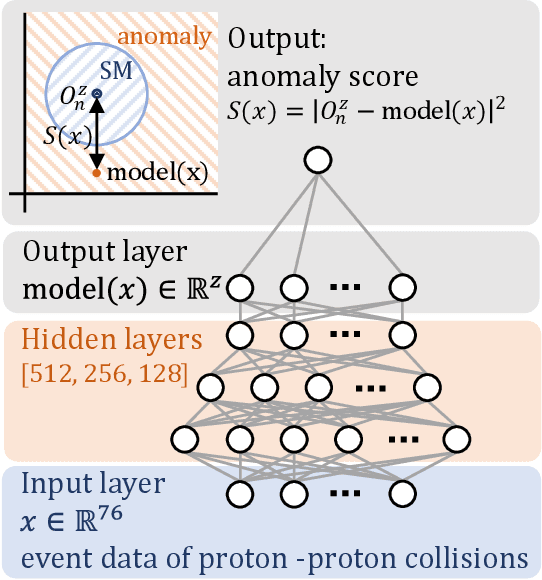
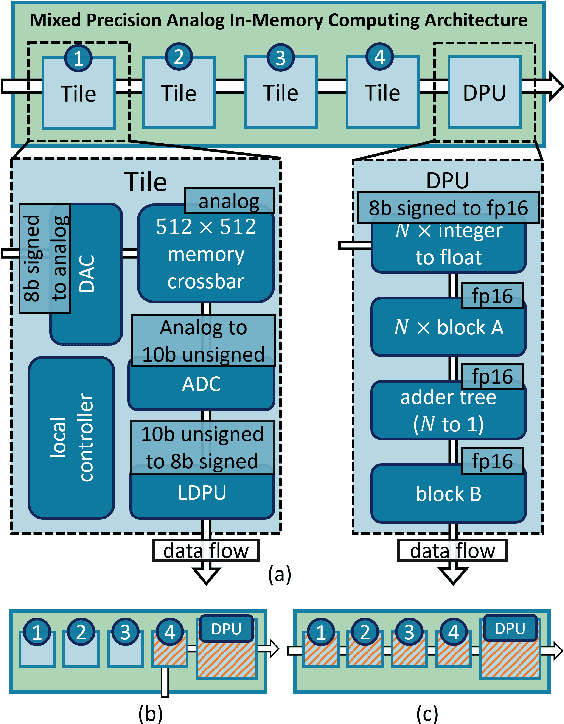
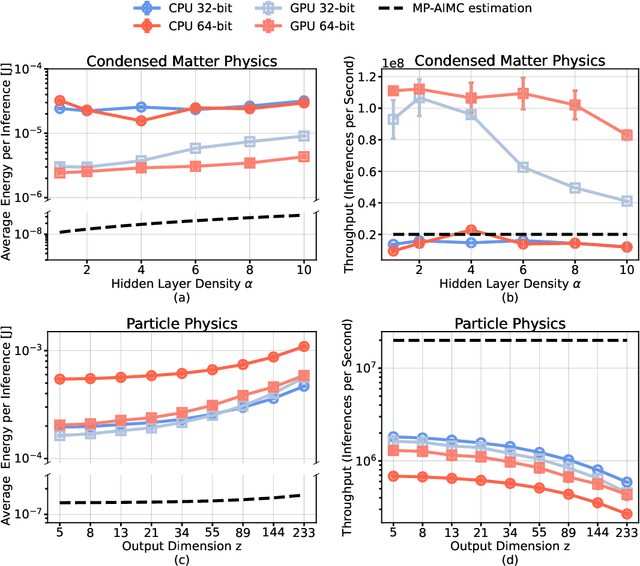
The massive use of artificial neural networks (ANNs), increasingly popular in many areas of scientific computing, rapidly increases the energy consumption of modern high-performance computing systems. An appealing and possibly more sustainable alternative is provided by novel neuromorphic paradigms, which directly implement ANNs in hardware. However, little is known about the actual benefits of running ANNs on neuromorphic hardware for use cases in scientific computing. Here we present a methodology for measuring the energy cost and compute time for inference tasks with ANNs on conventional hardware. In addition, we have designed an architecture for these tasks and estimate the same metrics based on a state-of-the-art analog in-memory computing (AIMC) platform, one of the key paradigms in neuromorphic computing. Both methodologies are compared for a use case in quantum many-body physics in two dimensional condensed matter systems and for anomaly detection at 40 MHz rates at the Large Hadron Collider in particle physics. We find that AIMC can achieve up to one order of magnitude shorter computation times than conventional hardware, at an energy cost that is up to three orders of magnitude smaller. This suggests great potential for faster and more sustainable scientific computing with neuromorphic hardware.

Motivating explanations in Bayesian networks using MAP-independence

In decision support systems the motivation and justification of the system's diagnosis or classification is crucial for the acceptance of the system by the human user. In Bayesian networks a diagnosis or classification is typically formalized as the computation of the most probable joint value assignment to the hypothesis variables, given the observed values of the evidence variables (generally known as the MAP problem). While solving the MAP problem gives the most probable explanation of the evidence, the computation is a black box as far as the human user is concerned and it does not give additional insights that allow the user to appreciate and accept the decision. For example, a user might want to know to whether an unobserved variable could potentially (upon observation) impact the explanation, or whether it is irrelevant in this aspect. In this paper we introduce a new concept, MAP- independence, which tries to capture this notion of relevance, and explore its role towards a potential justification of an inference to the best explanation. We formalize several computational problems based on this concept and assess their computational complexity.

On the computational power and complexity of Spiking Neural Networks

The last decade has seen the rise of neuromorphic architectures based on artificial spiking neural networks, such as the SpiNNaker, TrueNorth, and Loihi systems. The massive parallelism and co-locating of computation and memory in these architectures potentially allows for an energy usage that is orders of magnitude lower compared to traditional Von Neumann architectures. However, to date a comparison with more traditional computational architectures (particularly with respect to energy usage) is hampered by the lack of a formal machine model and a computational complexity theory for neuromorphic computation. In this paper we take the first steps towards such a theory. We introduce spiking neural networks as a machine model where---in contrast to the familiar Turing machine---information and the manipulation thereof are co-located in the machine. We introduce canonical problems, define hierarchies of complexity classes and provide some first completeness results.

A spiking neural algorithm for the Network Flow problem

It is currently not clear what the potential is of neuromorphic hardware beyond machine learning and neuroscience. In this project, a problem is investigated that is inherently difficult to fully implement in neuromorphic hardware by introducing a new machine model in which a conventional Turing machine and neuromorphic oracle work together to solve such types of problems. We show that the P-complete Max Network Flow problem is intractable in models where the oracle may be consulted only once (`create-and-run' model) but becomes tractable using an interactive (`neuromorphic co-processor') model of computation. More in specific we show that a logspace-constrained Turing machine with access to an interactive neuromorphic oracle with linear space, time, and energy constraints can solve Max Network Flow. A modified variant of this algorithm is implemented on the Intel Loihi chip; a neuromorphic manycore processor developed by Intel Labs. We show that by off-loading the search for augmenting paths to the neuromorphic processor we can get energy efficiency gains, while not sacrificing runtime resources. This result demonstrates how P-complete problems can be mapped on neuromorphic architectures in a theoretically and potentially practically efficient manner.

Finding dissimilar explanations in Bayesian networks: Complexity results

Finding the most probable explanation for observed variables in a Bayesian network is a notoriously intractable problem, particularly if there are hidden variables in the network. In this paper we examine the complexity of a related problem, that is, the problem of finding a set of sufficiently dissimilar, yet all plausible, explanations. Applications of this problem are, e.g., in search query results (you won't want 10 results that all link to the same website) or in decision support systems. We show that the problem of finding a 'good enough' explanation that differs in structure from the best explanation is at least as hard as finding the best explanation itself.

The Computational Complexity of Sensitivity Analysis and Parameter Tuning

While known algorithms for sensitivity analysis and parameter tuning in probabilistic networks have a running time that is exponential in the size of the network, the exact computational complexity of these problems has not been established as yet. In this paper we study several variants of the tuning problem and show that these problems are NPPP-complete in general. We further show that the problems remain NP-complete or PP-complete, for a number of restricted variants. These complexity results provide insight in whether or not recent achievements in sensitivity analysis and tuning can be extended to more general, practicable methods.