Improved Differential-neural Cryptanalysis for Round-reduced Simeck32/64

In CRYPTO 2019, Gohr presented differential-neural cryptanalysis by building the differential distinguisher with a neural network, achieving practical 11-, and 12-round key recovery attack for Speck32/64. Inspired by this framework, we develop the Inception neural network that is compatible with the round function of Simeck to improve the accuracy of the neural distinguishers, thus improving the accuracy of (9-12)-round neural distinguishers for Simeck32/64. To provide solid baselines for neural distinguishers, we compute the full distribution of differences induced by one specific input difference up to 13-round Simeck32/64. Moreover, the performance of the DDT-based distinguishers in multiple ciphertext pairs is evaluated. Compared with the DDT-based distinguishers, the 9-, and 10-round neural distinguishers achieve better accuracy. Also, an in-depth analysis of the wrong key response profile revealed that the 12-th and 13-th bits of the subkey have little effect on the score of the neural distinguisher, thereby accelerating key recovery attacks. Finally, an enhanced 15-round and the first practical 16-, and 17-round attacks are implemented for Simeck32/64, and the success rate of both the 15-, and 16-round attacks is almost 100%.

Improved Neural Distinguishers with (Related-key) Differentials: Applications in SIMON and SIMECK

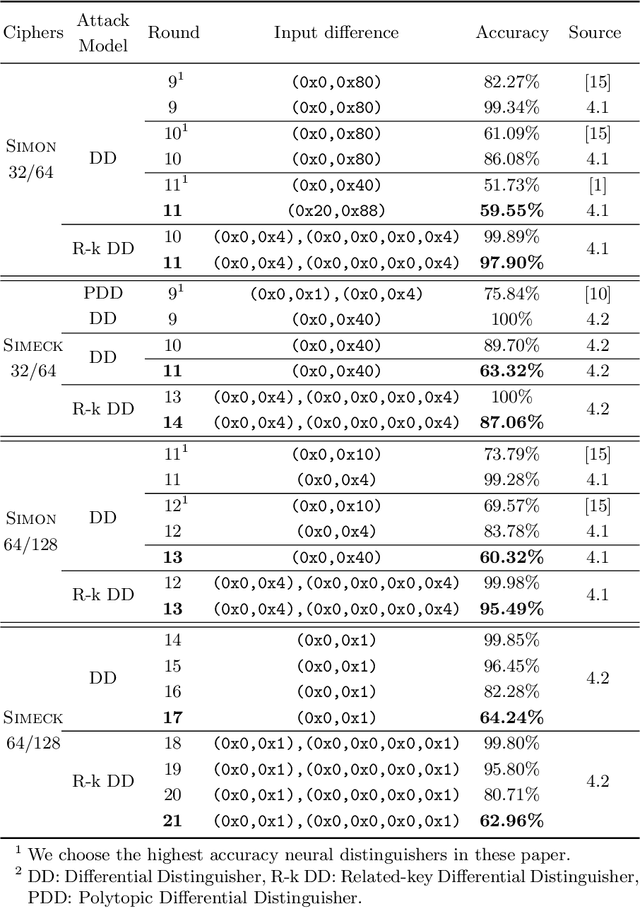
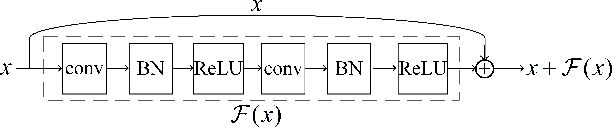
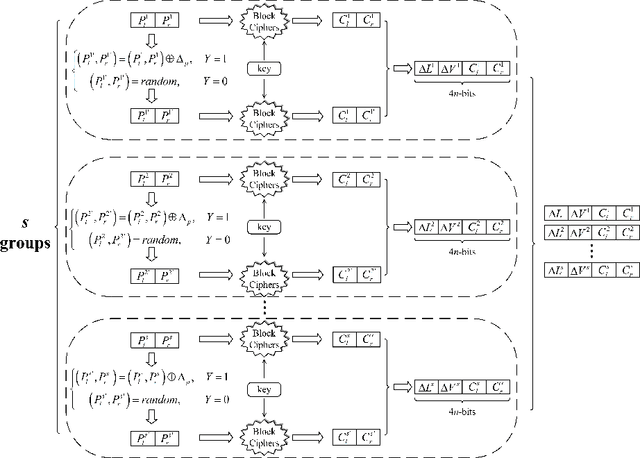
In CRYPTO 2019, Gohr made a pioneering attempt, and successfully applied deep learning to the differential cryptanalysis against NSA block cipher Speck32/64, achieving higher accuracy than the pure differential distinguishers. By its very nature, mining effective features in data plays a crucial role in data-driven deep learning. In this paper, in addition to considering the integrity of the information from the training data of the ciphertext pair, domain knowledge about the structure of differential cryptanalysis is also considered into the training process of deep learning to improve the performance. Besides, based on the SAT/SMT solvers, we find other high probability compatible differential characteristics which effectively improve the performance compared with previous work. We build neural distinguishers (NDs) and related-key neural distinguishers (RKNDs) against Simon and Simeck. The ND and RKND for Simon32/64 reach 11-, 11-round with an accuracy of 59.55% and 97.90%, respectively. For Simon64/128, the ND achieve an accuracy of 60.32% in 13-round, while it is 95.49% for the RKND. For Simeck32/64, ND and RKND of 11-, 14-round are obtained, reaching an accuracy of 63.32% and 87.06%, respectively. And we build 17-round ND and 21-round RKND for Simeck64/128 with an accuracy of 64.24% and 62.96%, respectively. Currently, these are the longest (related-key) neural distinguishers with higher accuracy for Simon32/64, Simon64/128, Simeck32/64 and Simeck64/128.