Jinshan Wu
Language Hierarchization Provides the Optimal Solution to Human Working Memory Limits
Jan 06, 2026Abstract:Language is a uniquely human trait, conveying information efficiently by organizing word sequences in sentences into hierarchical structures. A central question persists: Why is human language hierarchical? In this study, we show that hierarchization optimally solves the challenge of our limited working memory capacity. We established a likelihood function that quantifies how well the average number of units according to the language processing mechanisms aligns with human working memory capacity (WMC) in a direct fashion. The maximum likelihood estimate (MLE) of this function, tehta_MLE, turns out to be the mean of units. Through computational simulations of symbol sequences and validation analyses of natural language sentences, we uncover that compared to linear processing, hierarchical processing far surpasses it in constraining the tehta_MLE values under the human WMC limit, along with the increase of sequence/sentence length successfully. It also shows a converging pattern related to children's WMC development. These results suggest that constructing hierarchical structures optimizes the processing efficiency of sequential language input while staying within memory constraints, genuinely explaining the universal hierarchical nature of human language.
Quantum Inspired Word Representation and Computation
Apr 08, 2020
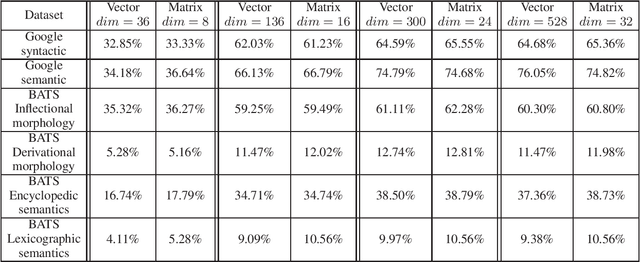
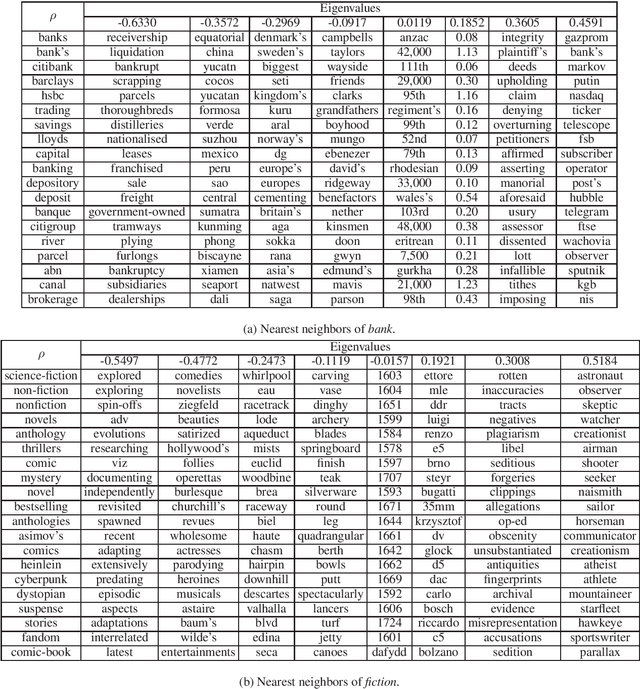
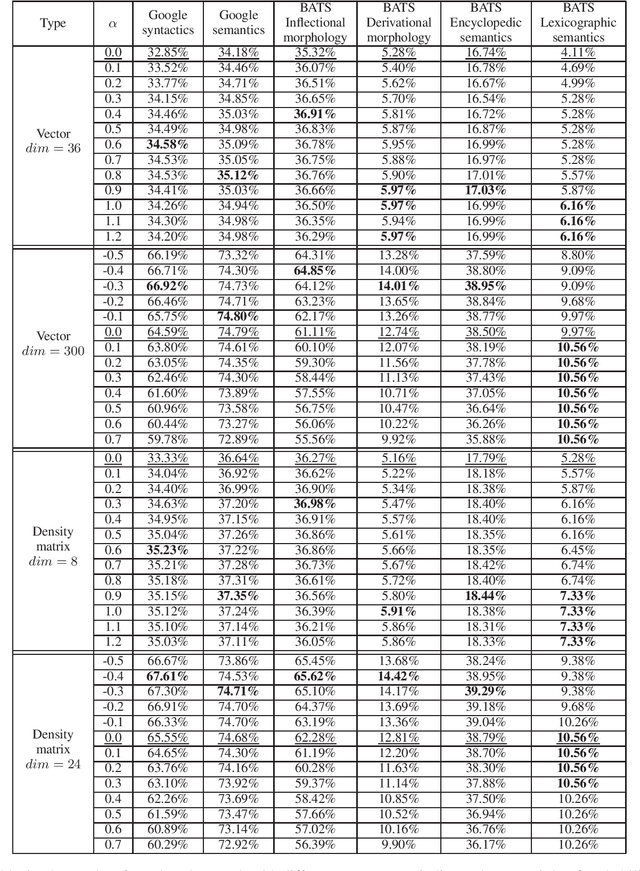
Abstract:Word meaning has different aspects, while the existing word representation "compresses" these aspects into a single vector, and it needs further analysis to recover the information in different dimensions. Inspired by quantum probability, we represent words as density matrices, which are inherently capable of representing mixed states. The experiment shows that the density matrix representation can effectively capture different aspects of word meaning while maintaining comparable reliability with the vector representation. Furthermore, we propose a novel method to combine the coherent summation and incoherent summation in the computation of both vectors and density matrices. It achieves consistent improvement on word analogy task.
Efficient learning strategy of Chinese characters based on network approach
Mar 07, 2013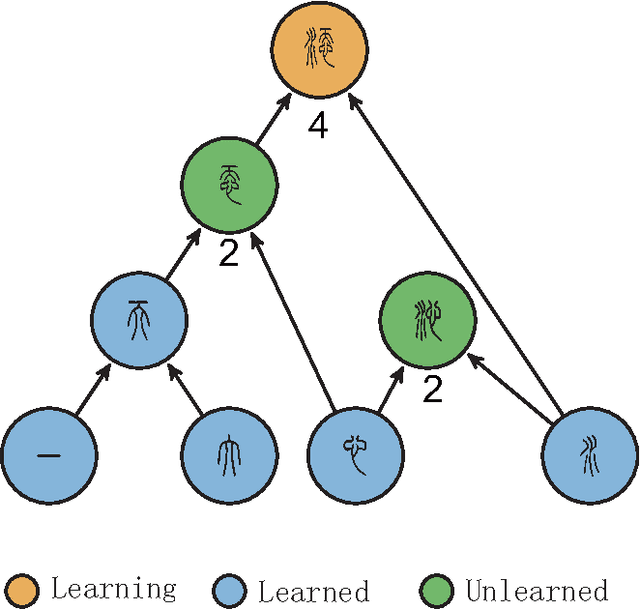
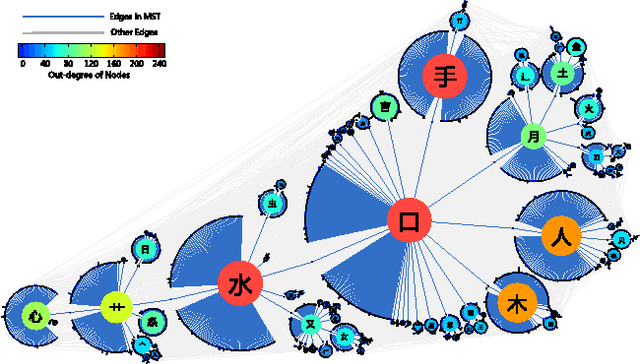
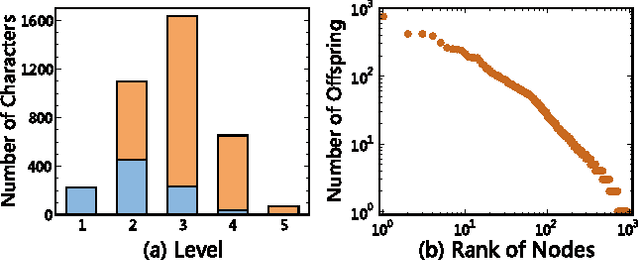
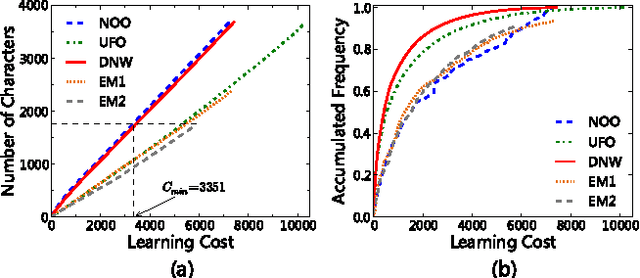
Abstract:Based on network analysis of hierarchical structural relations among Chinese characters, we develop an efficient learning strategy of Chinese characters. We regard a more efficient learning method if one learns the same number of useful Chinese characters in less effort or time. We construct a node-weighted network of Chinese characters, where character usage frequencies are used as node weights. Using this hierarchical node-weighted network, we propose a new learning method, the distributed node weight (DNW) strategy, which is based on a new measure of nodes' importance that takes into account both the weight of the nodes and the hierarchical structure of the network. Chinese character learning strategies, particularly their learning order, are analyzed as dynamical processes over the network. We compare the efficiency of three theoretical learning methods and two commonly used methods from mainstream Chinese textbooks, one for Chinese elementary school students and the other for students learning Chinese as a second language. We find that the DNW method significantly outperforms the others, implying that the efficiency of current learning methods of major textbooks can be greatly improved.
* 8 pages, 6 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge