Solve Large-scale Unit Commitment Problems by Physics-informed Graph Learning

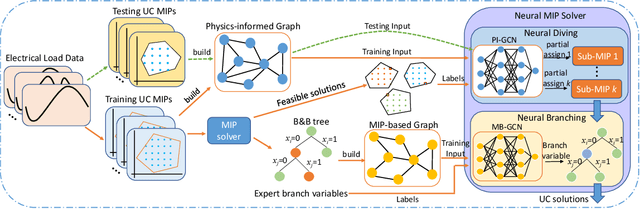
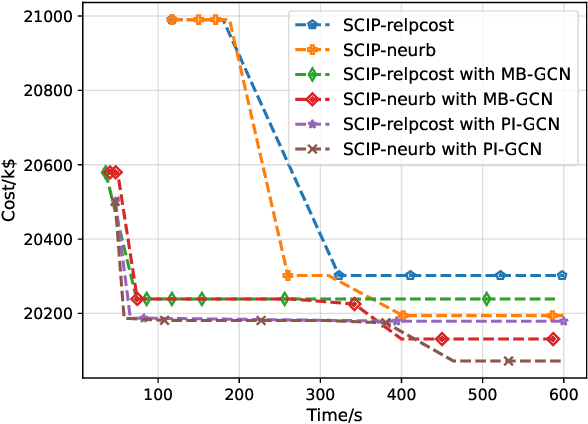
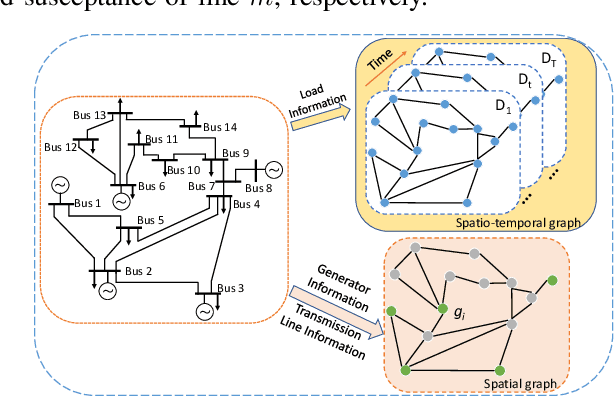
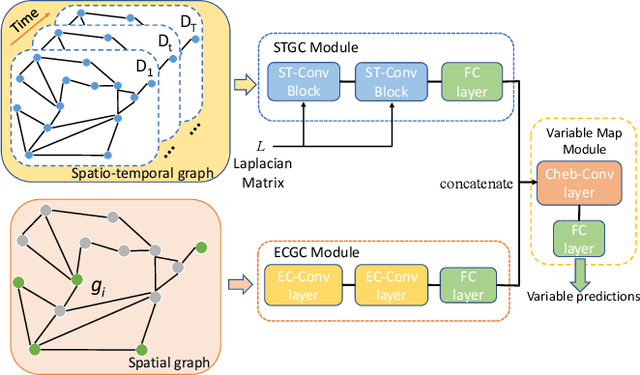
Unit commitment (UC) problems are typically formulated as mixed-integer programs (MIP) and solved by the branch-and-bound (B&B) scheme. The recent advances in graph neural networks (GNN) enable it to enhance the B&B algorithm in modern MIP solvers by learning to dive and branch. Existing GNN models that tackle MIP problems are mostly constructed from mathematical formulation, which is computationally expensive when dealing with large-scale UC problems. In this paper, we propose a physics-informed hierarchical graph convolutional network (PI-GCN) for neural diving that leverages the underlying features of various components of power systems to find high-quality variable assignments. Furthermore, we adopt the MIP model-based graph convolutional network (MB-GCN) for neural branching to select the optimal variables for branching at each node of the B&B tree. Finally, we integrate neural diving and neural branching into a modern MIP solver to establish a novel neural MIP solver designed for large-scale UC problems. Numeral studies show that PI-GCN has better performance and scalability than the baseline MB-GCN on neural diving. Moreover, the neural MIP solver yields the lowest operational cost and outperforms a modern MIP solver for all testing days after combining it with our proposed neural diving model and the baseline neural branching model.

An Optimization Method-Assisted Ensemble Deep Reinforcement Learning Algorithm to Solve Unit Commitment Problems

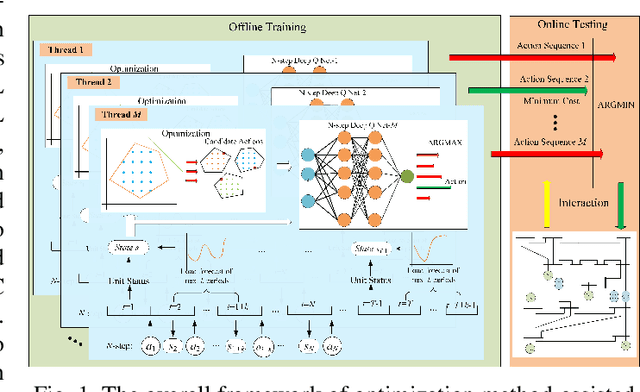
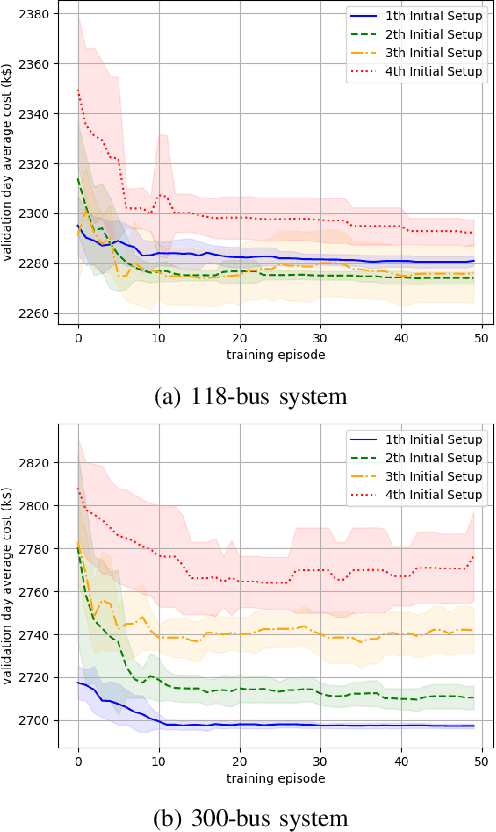
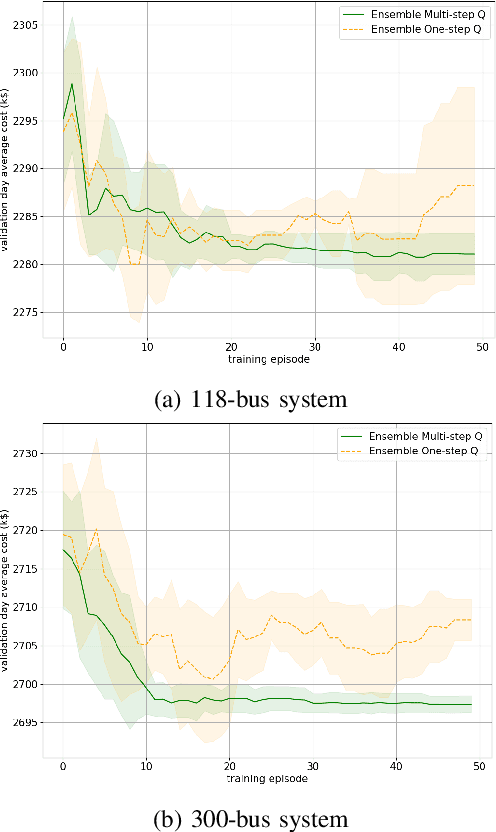
Unit commitment (UC) is a fundamental problem in the day-ahead electricity market, and it is critical to solve UC problems efficiently. Mathematical optimization techniques like dynamic programming, Lagrangian relaxation, and mixed-integer quadratic programming (MIQP) are commonly adopted for UC problems. However, the calculation time of these methods increases at an exponential rate with the amount of generators and energy resources, which is still the main bottleneck in industry. Recent advances in artificial intelligence have demonstrated the capability of reinforcement learning (RL) to solve UC problems. Unfortunately, the existing research on solving UC problems with RL suffers from the curse of dimensionality when the size of UC problems grows. To deal with these problems, we propose an optimization method-assisted ensemble deep reinforcement learning algorithm, where UC problems are formulated as a Markov Decision Process (MDP) and solved by multi-step deep Q-learning in an ensemble framework. The proposed algorithm establishes a candidate action set by solving tailored optimization problems to ensure a relatively high performance and the satisfaction of operational constraints. Numerical studies on IEEE 118 and 300-bus systems show that our algorithm outperforms the baseline RL algorithm and MIQP. Furthermore, the proposed algorithm shows strong generalization capacity under unforeseen operational conditions.