Solve Large-scale Unit Commitment Problems by Physics-informed Graph Learning
Paper and Code
Nov 26, 2023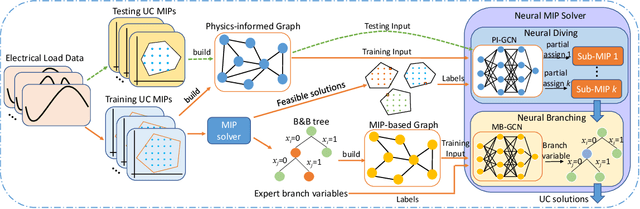
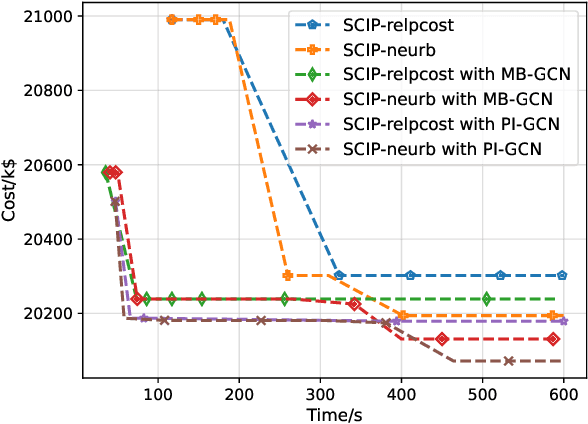
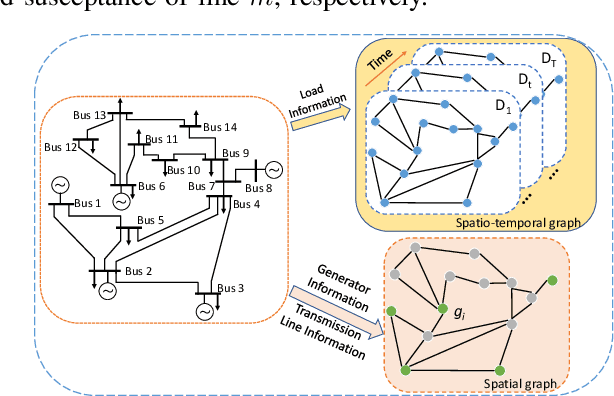
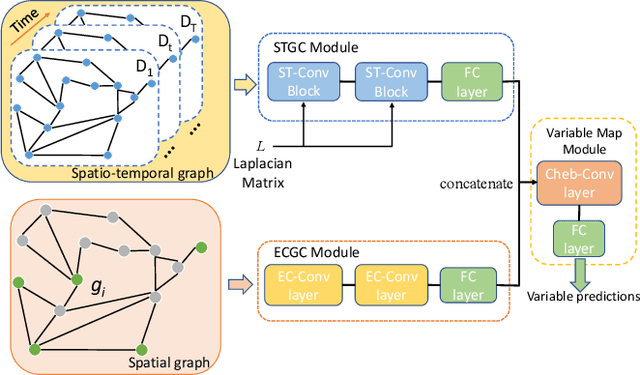
Unit commitment (UC) problems are typically formulated as mixed-integer programs (MIP) and solved by the branch-and-bound (B&B) scheme. The recent advances in graph neural networks (GNN) enable it to enhance the B&B algorithm in modern MIP solvers by learning to dive and branch. Existing GNN models that tackle MIP problems are mostly constructed from mathematical formulation, which is computationally expensive when dealing with large-scale UC problems. In this paper, we propose a physics-informed hierarchical graph convolutional network (PI-GCN) for neural diving that leverages the underlying features of various components of power systems to find high-quality variable assignments. Furthermore, we adopt the MIP model-based graph convolutional network (MB-GCN) for neural branching to select the optimal variables for branching at each node of the B&B tree. Finally, we integrate neural diving and neural branching into a modern MIP solver to establish a novel neural MIP solver designed for large-scale UC problems. Numeral studies show that PI-GCN has better performance and scalability than the baseline MB-GCN on neural diving. Moreover, the neural MIP solver yields the lowest operational cost and outperforms a modern MIP solver for all testing days after combining it with our proposed neural diving model and the baseline neural branching model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge